
試行回数を大きくしたとき二項分布は正規分布に近づいていくのか、Pythonでグラフを作成することで検証してみました。
二項分布のヒストグラムと正規分布のグラフを重ねて観察する実験①と、実際にどちらも確率を算出して確率が近似できているのかの実験②の2つを行っています。
目次
正規分布のコード【Python】
正規分布のPythonコード
次のコードをコピペすれば正規分布をPythonで描写できます。母平均と母標準偏差のところの数字を変えて、必要な正規分布を作成してください。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm #normは正規分布
mu = 50 # 母平均
sigma = 10 # 母標準偏差
#正規分布を表示
X = np.arange(mu-5*sigma, mu+5*sigma, 0.1)
Y = norm.pdf(X, mu, sigma)
plt.plot(X, Y, color="orange", label = "Normal-distribution")
#グラフの表示
plt.legend() #凡例表示
plt.show()正規分布の表示結果

【実験①】二項分布と正規分布の見た目の観察
実験開始(Pythonコード)
試行回数 $n$ の二項分布 $B(n, p)$ と正規分布 $N(np, np(1-p))$ の違いを観察するコードを紹介します。
今回のコードでは、二項分布 $B(100, 0.3)$ と 正規分布 $N(30, 21)$ を比較しています。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import binom
from scipy.stats import norm
# 二項分布の情報
n = 100 # Number of trials
p = 0.3 # Probability of success
# Plot the binomial distribution
x_values = np.arange(0, n + 1)
binomial_probs = binom.pmf(x_values, n, p)
plt.bar(x_values, binomial_probs, color='y', alpha=0.7, label = "Binomial-distribution")
#正規分布を表示
mu = n*p # 母平均
sigma = np.sqrt(n*p*(1-p)) # 母標準偏差
X = np.arange(mu-3*sigma, mu+3*sigma, 0.1)
Y = norm.pdf(X, mu, sigma)
plt.plot(X, Y, color="b", label = "Normal-distribution")
# Other Informations
plt.legend() #凡例表示
plt.xlabel("Number of Successes")
plt.ylabel("Probability")
plt.title(f"Binomial Distribution (n={n}, p={p})")
plt.grid(True)
plt.show()試行結果
試行回数が $n=100$ のときと、他のいくつかの場合で二項分布のヒストグラムと、正規分布を重ねて描写しています。
$B(100, 0.3)$ と $N(30, 21)$ の比較

$n = 100$ のときは,二項分布(黄色)はかなり密なので,正規分布が近似になってそう。
$B(40, 0.3)$ と $N(12, 8.4)$ の比較

$n=40$ では,隙間が見えるが,まだ密なので良い感じで近似になってそう。
$B(30, 0.3)$ と $N(9, 6.3)$ の比較

$n=30$ のときも,まだ正規分布で近似できていると言ってもよさそう。
$B(10, 0.3)$ と $N(3, 2.1)$ の比較

$n=10$ のときは,二項分布の左右非対称性が目立つので,正規分布の対称性と相性が悪そう。
$B(5, 0.3)$ と $N(1.5, 1.05)$ の比較

$n=5$ では,だいぶ左右非対称のスカスカなので,近似の精度が良いのか?って思う。
以上から、試行回数が増えれば、二項分布と正規分布は一致していくと考えてもよさそうですね。
【実験②】二項分布と正規分布の確率の数値比較
二項分布で $P(a<X<b)$ の確率を計算したときと, 正規分布で $P(a<X<b)$ の計算をしたときの値の比較をして近似できているか調べたいと思いました。
実験開始(Pythonコード)
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import binom
from scipy.stats import norm
from scipy import stats
import math
# 試行回数と成功確率
n = 100 # 試行回数
p = 0.5 # 成功確率
A = 60 # [正規分布]A以上の所の確率を求める [二項分布]Aからnまでの確率の和を求める
# 二項分布を表示
x_values = np.arange(0, n)
binomial_probs = binom.pmf(x_values, n, p)
plt.bar(x_values, binomial_probs, color='y', alpha=0.7, label = "Binomial-distribution")
#正規分布を表示
mu = n*p # 母平均
sigma = np.sqrt(n*p*(1-p)) # 母標準偏差
X = np.arange(0, n+1, 0.1)
Y = norm.pdf(X, mu, sigma)
plt.plot(X, Y, color="b", label = "Normal-distribution")
# Other Informations
plt.legend() #凡例表示
plt.xlabel("Number of Successes")
plt.ylabel("Probability")
plt.title(f"Binomial Distribution (n={n}, p={p})")
plt.grid(True)
plt.fill_between(X[X >= A], Y[X >= A])
plt.show()
def sum_binomial_probs(n, p, m):
total_prob = 0.0
for k in range(math.ceil(m), n+1):
prob = binom.pmf(k, n, p) # 二項分布の確率質量関数を使用
total_prob += prob
return total_prob
sum_prob = sum_binomial_probs(n, p, A)
print(f"[二項分布]{n} 回試行して, 成功回数が {A} 回以上の確率は約{sum_prob*100: .5f}% です.")
probability = 1 - stats.norm.cdf(x = A, loc=mu, scale=sigma)
# 結果の表示
print(f"[正規分布]成功回数が{A}回以上になる確率は約{probability * 100:.5f}%です。")試行結果
実際に上のPythonコードを実行すると、次の出力が得られます。
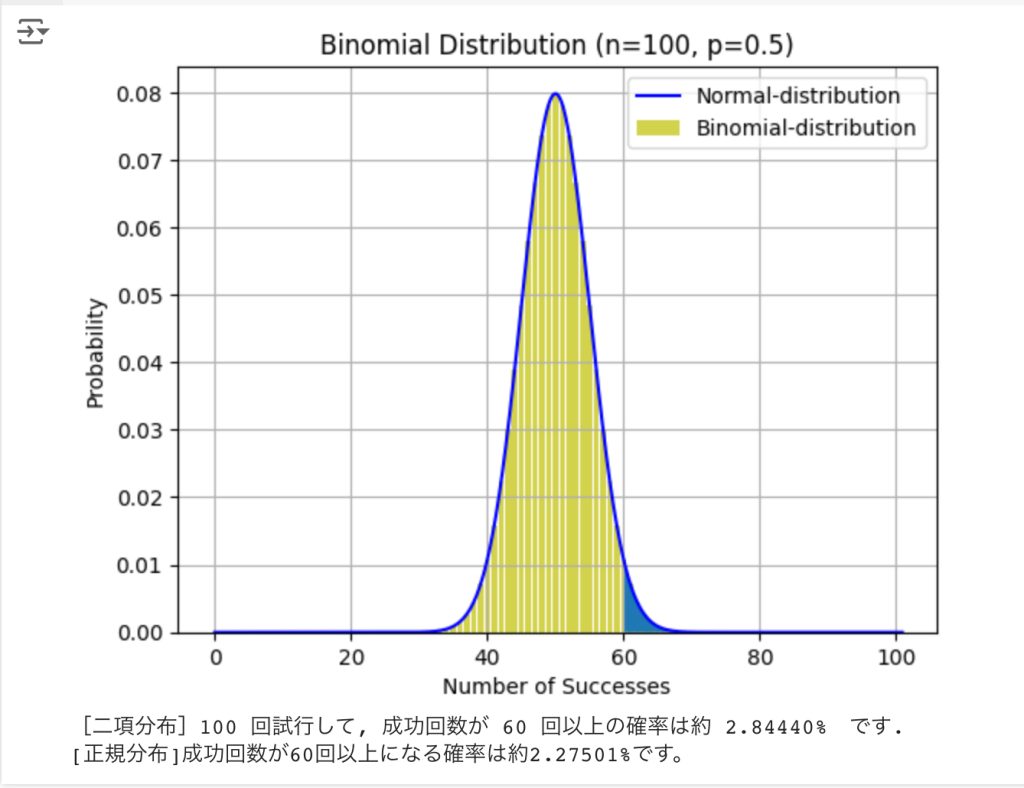
試行回数 $n=100$ のとき、成功回数が60回以上の確率を調べています。
黄色の二項分布の方は、約2.84%(0.0284)の確率で、青色の正規分布の方は約2.27%(0.0227)の確率でした。
「近似している」とは言えない感じですね。
「だいたい同じ」ということもできなくもないです。
でも、もっと試行回数が大きければ、もっと良い近似ができそうな気はします。
おおよその値を出すだけならば、どちらかの計算で代用しても良さそうです。
いろいろと数字を変えて、やってみてね!


