• まとめ
  • 目次
  • ①コード
  • ②観察
  • ③理解

「正規分布」とは

実験や製造などの誤差がつくる最も自然な確率分布のこと。

記号

$N(m, \sigma^2)$ は平均値 $m$, 標準偏差 $\sigma$ の正規分布を表す.

A. 確率密度関数

$$f(x) = \frac{1}{\sqrt{2 \pi}\sigma} e^{-\frac{(x-m)^2}{2\sigma^2}}$$

B. 性質（確率の目安）

  1. $P(m-\sigma \leqq X \leqq m+\sigma)$ $\fallingdotseq 0.68$
  2. $P(m-2\sigma \leqq X \leqq m+2\sigma)$ $\fallingdotseq 0.95$
  3. $P(m-3\sigma \leqq X \leqq m+3\sigma)$ $\fallingdotseq 0.99$

C. 標準化（変数変換）

確率変数 $X$ が $N(m,\sigma^2)$ に従うとき, $\displaystyle Z=\frac{X-m}{\sigma}$ は $N(0,1^2)$ に従う.

ポイント解説

イメージ

$n$ が大きな二項分布は正規分布で近似できます。偏差値は正規分布です。

二項分布
偏差値

A

$N(0,1^2)$ を標準正規分布といいます。

$$f(z) = \frac{1}{\sqrt{2 \pi}} e^{-\frac{z^2}{2}}$$

無理数 $e = 2.718 \cdots$ はネイピア数と呼ばれます。

B

平均値 $m$ から $\pm2\sigma$ や $\pm3\sigma$ 以上離れたデータを外れ値と定義することがあります。

Pythonコード

正規分布のコード

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm #normは正規分布

mu = 50 # 母平均
sigma = 10 # 母標準偏差

#正規分布を表示
X = np.arange(mu-5*sigma, mu+5*sigma, 0.1)
Y = norm.pdf(X, mu, sigma)
plt.plot(X, Y, color="orange", label = "Normal-distribution")

#グラフの表示
plt.legend() #凡例表示
plt.show()

正規分布の観察

今日の授業

二項分布 $B(n, p)$ が正規分布 $N(np, np(1-p))$ に近似できるってなったけど本当なの？

ゴルトンボード

二項分布と正規分布の違い

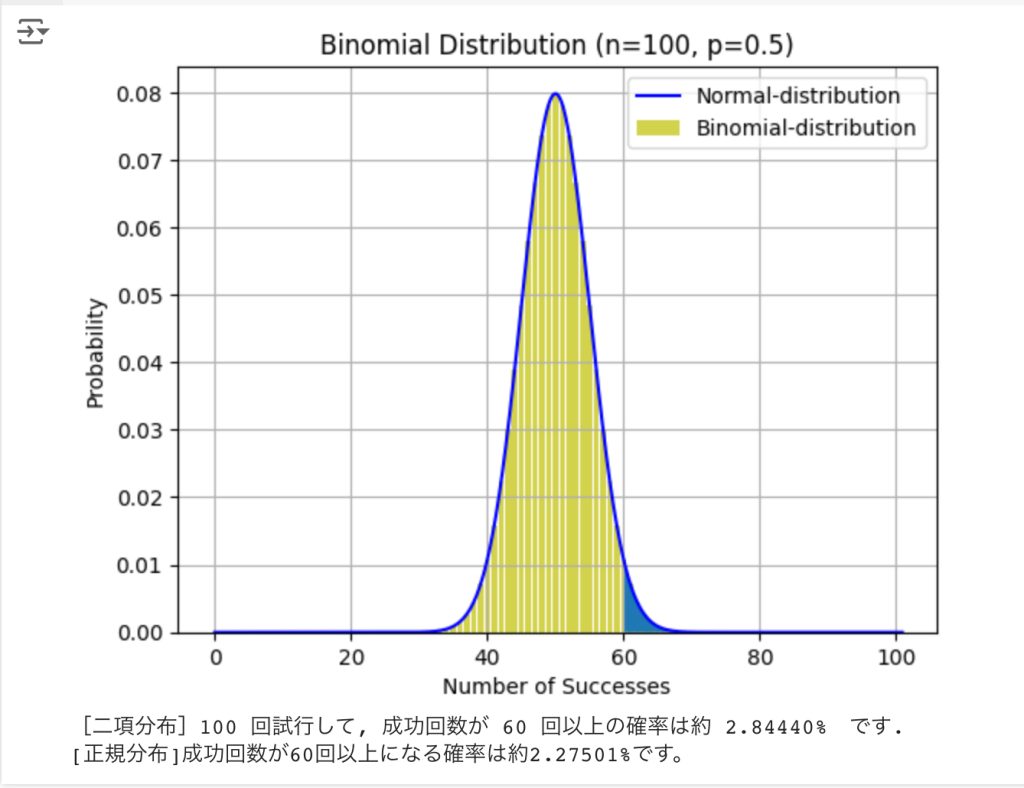
試行回数 $n$ の二項分布 $B(n, p)$ と正規分布 $N(np, np(1-p))$ の違いを観察する。

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import binom
from scipy.stats import norm

# 二項分布の情報
n = 100  # Number of trials
p = 0.3  # Probability of success

# Plot the binomial distribution
x_values = np.arange(0, n + 1)
binomial_probs = binom.pmf(x_values, n, p)
plt.bar(x_values, binomial_probs, color='y', alpha=0.7, label = "Binomial-distribution")

#正規分布を表示
mu = n*p # 母平均
sigma = np.sqrt(n*p*(1-p)) # 母標準偏差
X = np.arange(mu-3*sigma, mu+3*sigma, 0.1)
Y = norm.pdf(X, mu, sigma)
plt.plot(X, Y, color="b", label = "Normal-distribution")

# Other Informations
plt.legend() #凡例表示
plt.xlabel("Number of Successes")
plt.ylabel("Probability")
plt.title(f"Binomial Distribution (n={n}, p={p})")
plt.grid(True)
plt.show()

試行結果

$n = 100$ のときは，二項分布(黄色)はかなり密なので，正規分布が近似になってそう。

$n=40$ では，隙間が見えるが，まだ密なので良い感じで近似になってそう。

$n=30$ のときも，まだ正規分布で近似できていると言ってもよさそう。

$n=10$ のときは，二項分布の左右非対称性が目立つので，正規分布の対称性と相性が悪そう。

$n=5$ では，だいぶ左右非対称のスカスカなので，近似の精度が良いのか？って思う。

数値的な比較

二項分布で $P(a<X<b)$ の確率を計算したときと, 正規分布で $P(a<X<b)$ の計算をしたときの値の比較をして近似できているか調べましょう。

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import binom
from scipy.stats import norm
from scipy import stats
import math

# 試行回数と成功確率
n = 100  # 試行回数
p = 0.5  # 成功確率
A = 60 # [正規分布]A以上の所の確率を求める [二項分布]Aからnまでの確率の和を求める

# 二項分布を表示
x_values = np.arange(0, n)
binomial_probs = binom.pmf(x_values, n, p)
plt.bar(x_values, binomial_probs, color='y', alpha=0.7, label = "Binomial-distribution")

#正規分布を表示
mu = n*p # 母平均
sigma = np.sqrt(n*p*(1-p)) # 母標準偏差
X = np.arange(0, n+1, 0.1)
Y = norm.pdf(X, mu, sigma)
plt.plot(X, Y, color="b", label = "Normal-distribution")

# Other Informations
plt.legend() #凡例表示
plt.xlabel("Number of Successes")
plt.ylabel("Probability")
plt.title(f"Binomial Distribution (n={n}, p={p})")
plt.grid(True)
plt.fill_between(X[X >= A], Y[X >= A])
plt.show()

def sum_binomial_probs(n, p, m):
    total_prob = 0.0
    for k in range(math.ceil(m), n+1):
        prob = binom.pmf(k, n, p)  # 二項分布の確率質量関数を使用
        total_prob += prob
    return total_prob

sum_prob = sum_binomial_probs(n, p, A)
print(f"［二項分布］{n} 回試行して, 成功回数が {A} 回以上の確率は約{sum_prob*100: .5f}%　です.")

probability = 1 - stats.norm.cdf(x = A, loc=mu, scale=sigma)
# 結果の表示
print(f"[正規分布]成功回数が{A}回以上になる確率は約{probability * 100:.5f}%です。")

正規分布の理解

  1. 正規分布の確率密度関数
  2. 正規分布の期待値と分散
  3. 正規分布の再帰性（準備中）

正規分布の確率密度関数

正規分布は英語でNormal distributionです。

正規分布

$m \in \mathbf{R}$, $\sigma > 0$ とする。次を確率密度関数とする確率分布を正規分布という。

$$f(x) = \frac{1}{\sqrt{2 \pi}\sigma} e^{-\frac{(x-m)^2}{2\sigma^2}}$$

この正規分布を $N(m, \sigma^2)$ と書く。

確率密度関数とは，$X$ の分布曲線 $y = f(x)$ であって，以下を満たすものである。

  • $0 \leqq f(x)$
  • $P(a \leqq X \leqq b) = \int_a^b f(x) dx$
  • $\int_a^b f(x) dx=1$

この確率分布の期待値は $m$, 分散は $\sigma^2$ に一致します。

確かめること．

確率密度関数であることを示す。必要条件としての積分が1であることを示す。

$$\displaystyle \int_{-\infty}^{\infty} \frac{1}{\sqrt{2 \pi}\sigma} e^{-\frac{(x-m)^2}{2\sigma^2}} dx=1$$

基本的なガウス積分の公式を仮定します。

$$\displaystyle \int_{-\infty}^{\infty} e^{-t^2} dx=\sqrt{\pi}$$

証明．

被積分関数について, 変数変換 $\displaystyle t = \frac{x-m}{\sqrt{2}\sigma}$ をする. $dt = \displaystyle \frac{1}{\sqrt{2} \sigma}dx$ である.

$\begin{array}{ll}
\displaystyle \int_{-\infty}^{\infty} f(x) dx & \displaystyle = \int_{-\infty}^{\infty} \frac{1}{\sqrt{2 \pi}\sigma} e^{-\frac{(x-m)^2}{2\sigma^2}} dx \\
& \displaystyle = \int_{-\infty}^{\infty} \frac{1}{\sqrt{2 \pi}\sigma} e^{-\left( \frac{x-m}{\sqrt{2}\sigma} \right)^2} dx \\
& \displaystyle= \int_{-\infty}^{\infty} \frac{1}{\sqrt{2 \pi}\sigma} e^{-t^2}( \sqrt{2} \sigma) dt \\
& \displaystyle= \int_{-\infty}^{\infty} \frac{1}{\sqrt{\pi}} e^{-t^2}dt \\
& \displaystyle= \frac{1}{\sqrt{\pi}} \int_{-\infty}^{\infty} e^{-t^2}dt \\
& \displaystyle= \frac{1}{\sqrt{\pi}} \cdot \sqrt{\pi} \\
& = 1. \\
\end{array}$

正規分布の期待値と分散

正規分布の統計量

$X \sim N(m, \sigma^2)$ のとき，期待値と標準偏差は次の通りである。

$$E(X) = m, \ \ \sigma(X) = \sigma$$

連続型確率分布の期待値 $E(X)$ と分散 $V(X)$ は次式で定義される：

$$E(X) = \int_{-\infty}^{\infty} xf(x) dx $$

$$V(X) = \int_{-\infty}^{\infty} (x-E(X))^2f(x) dx $$

計算する

準備中

正規分布の再帰性

定義.　確率変数 $X$ と $Y$ がお独立に正規分布 $N(\mu_1, \sigma_1^2)$，$N(\mu_2, \sigma_2^2)$ にそれぞれ従うとき，次が成り立つ：

$$X + Y \sim N(\mu_1 + \mu_2, \sigma_1^2 + \sigma_2^2).$$

・・・準備中

ネタ集め（参考文献）

カテゴリー
さいえんてぃすと
タグ

コメントをどうぞ

前の記事
二項分布について
2024-05-16
次の記事
母集団と標本分布について
2024-07-07