- 表紙
- まとめ

数学のまとめノート
「双曲線」とは
2次式で表される曲線のうち、双子になる曲線のこと。
定義
2点からの距離の差が一定の点の軌跡を双曲線という.
A. 横方向の双曲線
- 2点間の距離の差: $2a$
- $\displaystyle \frac{x^2}{a^2} - \frac{y^2}{b^2}=1$
- 頂点: $(a, 0)$, $(-a,0)$
- 焦点: $(c, 0)$, $(-c,0)$
- 離心率: $e=c/a$
- 焦点 $(ae, 0)$, 準線: $x=a/e$
B. 縦方向の双曲線
- 2点間の距離の差: $2b$
- $\displaystyle \frac{x^2}{a^2} - \frac{y^2}{b^2}=-1$
- 頂点: $(0, b)$, $(0, -b)$
- 焦点: $(0, c)$, $(0, -c)$
- 離心率: $e=c/b$
- 焦点 $(0, be)$, 準線: $y=b/e$
C. 双曲線の漸近線
双曲線には漸近線が存在する: $\displaystyle y =\frac{b}{a} x$, $\displaystyle y = - \frac{b}{a} x$
D. 双曲線の接線方程式
A.の双曲線上の $(x_0, y_0)$ を通る接線の方程式: $\displaystyle \frac{x_0}{a^2}x - \frac{y_0}{b^2}y = 1$
離心率
双曲線の離心率 $e$ は (焦点間の距離)/(頂点間の距離)である. $1<e$ である.
ポイント解説
イメージ
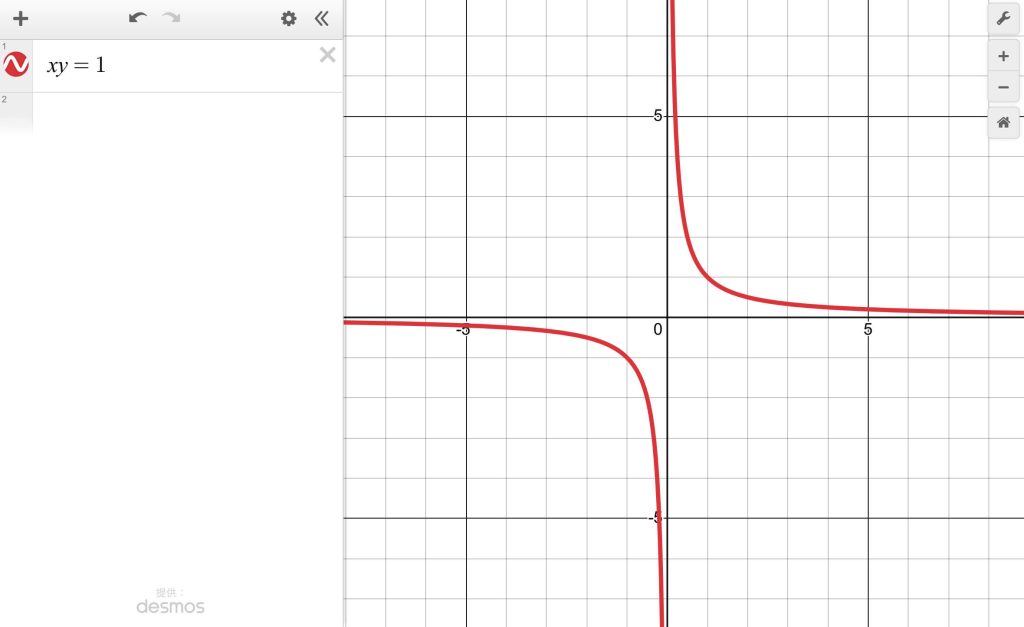
反比例 $xy=c$ のグラフは双曲線である;
定義
距離の差を $2a$, 焦点を $\mathrm{F}$ と $\mathrm{F}'$, 動点を $\mathrm{P}$ とすると, $|\mathrm{PF} - \mathrm{PF'}| = 2a$ となる。
離心率
(焦点からの距離)と(準線からの距離の比) が $e:1$ になる点の軌跡は双曲線である。
A・B
$c^2 = a^2 + b^2$ が成り立つ。
媒介変数表示(A)
三角関数の相互関係 $\frac{1}{\cos^2 \theta} = 1 + \tan^2 \theta$ により導かれる。$$(x,y) \displaystyle =\left(\frac{a}{\cos \theta}, \ b \tan \theta \right)$$

