因数分解について

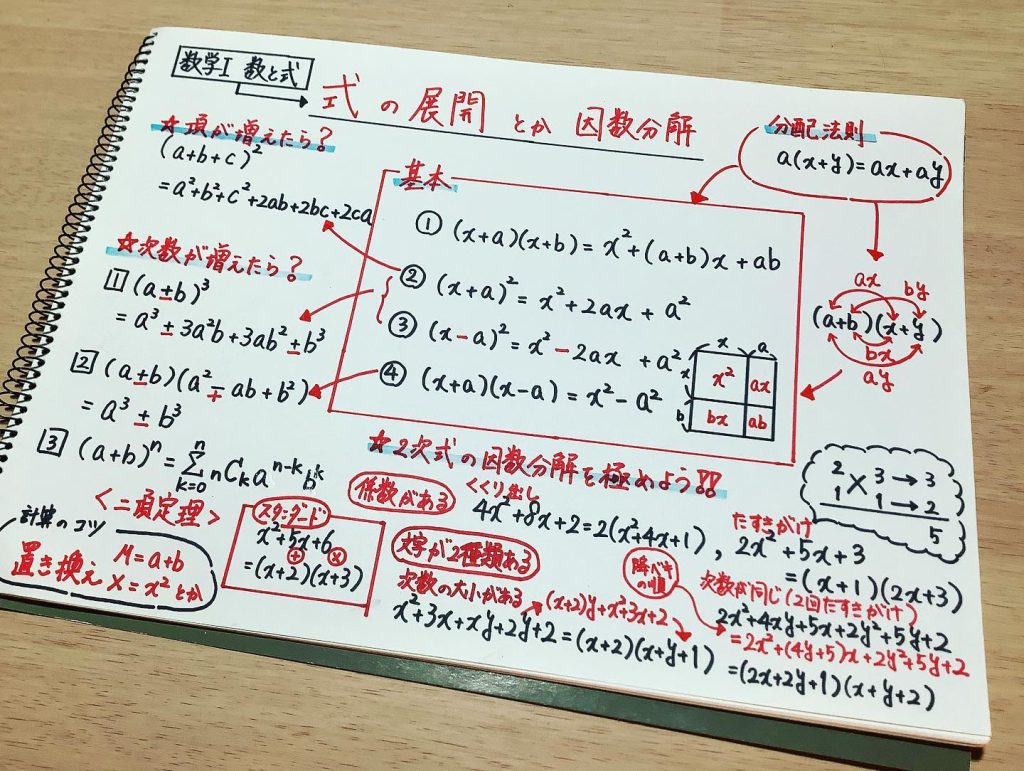
数学のまとめノート

「因数分解」とは

式の展開の逆の計算で、式を次数のより低い式の積で表すこと。

共通因数でくくる

$Ax + Ay = A(x+y)$

A. 2次式の因数分解（公式）

1. $x^2 + (a+b)x + ab$ $= (x+a)(x+b)$
2. $x^2 + 2ax + a^2= (x + a)^2$, $x^2 - 2ax + a^2= (x - a)^2$
3. $x^2 - a^2$ $= (x+a)(x-a)$

B. 3次式の因数分解（公式）

1. $x^3 + 3ax^2 + 3a^2x+ a^3 = (x + a)^3$, $x^3 - 3ax^2 + 3a^2x - a^3 = (x - a)^3$
2. $x^3 + a^3= (x + a)(x^2 - ax + a^2)$, $x^3 - a^3= (x - a)(x^2 + ax + a^2)$
3. $a^3 + b^3 + c^3 - 3abc$ $=(a+b+c)(a^2 + b^2 + c^2 - ab-bc-ca)$

除法

$P(x) \div A(x) = Q(x)$ $\Rightarrow$

$P(x) = A(x)Q(x)$

(因数分解)

C. $n$次式の因数分解（公式）

1. $x^n + {}_n\mathrm{C}_1 x^{n-1}a + \cdots + {}_n\mathrm{C}_{n-1}xa^{n-1} + a^n$ $= (x+a)^n$
2. $x^n - a^n$ $= (x - a)(x^{n-1} + x^{n-2}a + \cdots + x a^{n-2} + a^{n-1})$

ポイント解説

係数を簡単にする

ために共通因数をくくることもある。

A

長方形の縦と横の辺の長さを求める意味をもつ。

たすきがけ

計算例；$2x^2 + 5xy + 3y^2$ $=(2x+3y)(x+y)$

$$\begin{array}{ccccc}
2x& & 3y& \mathrm{-}&3xy \\
& \times & &&+ \\
x & & y & \mathrm{-} &2xy \\ \hline
2x^2 & & 3y^2 & & 5xy
\end{array}$$

除法

多項式 $P(x)$ が $A(x)$ で割り切れ, 商が $Q(x)$ という意味である.

因数定理

多項式 $P(x)$ と複素数 $\alpha$ について,

$P(\alpha) = 0$

ならば

$P(x)$ は $x - \alpha$ を因数

にもつ。

発展

任意の多項式は少なくとも1つの複素数根を持つ（代数学の基本定理）。

折り紙

因数分解の知識をオリガミ（折り紙）で体験します。

応用力を磨きたい人にオススメです！

高校数学の単元学習、普段の勉強を楽しく取り組みたい人にもオススメです。

たすきがけと折り紙

$2x^2 +5xy +3y^2 =(x+y)(2x+3y)$

「たすき」は使っていないので、ただの因数分解です（笑）

共通因数くくり出し

$4x^2 +8xy +4y^2 =4(x+y)^2$

4つに分けて！

次数の大小に着目し整理する

$x^2 +3x +xy +2y +2 =(x+y+1)(x+2)$

２回たすきがけするやつ

$2x^2 +4xy +5x+2y^2+5y +2$

$2x^2 +4xy +5x+2y^2+5y +2=(2x+2y+1)(x+y+2)$

おまけ（平方完成と折り紙）

$x^2 +3x =(x + 1.5)^2 -1.5^2$

以上です！

オリガミ（折り紙）で式の展開！

式の展開の知識をオリガミ（折り紙）で体験します。 応用力を磨きたい人にオススメです！ 高校数学の単元学習、普段の勉強を楽しく取り組みたい人にもオススメです。 目次…

ますレッスン教室

オリガミ（折り紙）で因数分解、平方完成！

因数分解の知識をオリガミ（折り紙）で体験します。 応用力を磨きたい人にオススメです！ 高校数学の単元学習、普段の勉強を楽しく取り組みたい人にもオススメです。 目次…

ますレッスン教室

オリガミ（折り紙）で3乗の立方公式！

式の展開と因数分解の３乗の計算の知識をオリガミ（折り紙）で体験します。 応用力を磨きたい人にオススメです！ 高校数学の単元学習、普段の勉強を楽しく取り組みたい人…

ますレッスン教室

Python

プログラミングで「たすきがけ」をしましょう。

PythonのSymPyを利用して、「式の展開」をする方法と「因数分解」をする方法を紹介します。

※Colaboratory環境で行っています。

例題として次の式を計算します。$$2x^2 + 5xy + 3y^2$$

Pythonで文字式の計算をする方法

SymPyについて

Pythonで文字を含む式の計算をするためには「sympy」を利用します。

Google Colaoratoryを利用する方は、「sympy」は初めからインストールされているので、すぐに文字式の計算をすることができます。

SymPy自体は「式の展開」や「因数分解」だけではなく、方程式を解くなど代数的な計算全般をカバーしています。

Sympyを使う

Pythonで文字を含む式の計算をするために、「sympy」をインポートします。

次のように入力します。

import sympy

SymPyの利用方法として、あらかじめ計算に使う「文字」を「シンボル（記号）」として定義しておく必要があります。

今回は、xとｙを使うので、2つのシンボルを定義します。

x = sympy.Symbol('x')
y = sympy.Symbol('y')

以上で、x と y が文字として利用できるようになりました。

ここまでのまとめです。

import sympy

x = sympy.Symbol('x')
y = sympy.Symbol('y')

この命令を実行（launch）しておきましょう。

※何も起こらなければOKです。

Pythonで式の展開と因数分解

SymPyで式を定義する

例題 $2x^2 + 5xy + 3y^2$ をPythonに入力します。この式を P と置きます。

次のように入力して実行してください。

P = 2*x**2 + 5*x*y + 3*y**2
print(P)

2*x**2 + 5*x*y + 3*y**2

このように出力されれば、ちゃんと P が入力できたことになります。

念のため、Pythonでの演算を掲載しておきます。

Sympyで因数分解する

式 P を定義しました。因数分解（たすきがけ）ができるので、Pythonに計算してもらいましょう。

Pythonで因数分解を行うためには、次のように入力します。

Q = sympy.factor(P)
print(Q)

このように入力して、実行すると、

(x + y)*(2*x + 3*y)

と表示されました。

因数分解成功です！やったね✌

なお、因数分解を行うだけであれば、次の入力だけで構いません。

print(sympy.factor(P))

SymPyで式の展開をする

Sympyで因数分解をすることができました。

式の展開もしたいですね。

Pを因数分解した式がQの式でした。

Q = (x+y)(2x+3y)

Qを展開するためには、次のように入力してください。

print(sympy.expand(Q))

2*x**2 + 5*x*y + 3*y**2

Qが展開された式である P が出力されれば成功ですね。

SymPyでLaTeX表示（おまけ）

SymPyを利用することで、式の展開も因数分解（たすきがけ）も行うことができました。

でも、扱っている式が少し見にくいのが少し嫌です。

最後に、LaTeX表示させてみます。Google Colaboratoryの場合は、非常に簡単に行うことが可能です。

次のように入力してください。

display(P)
display(Q)

結果としては、次のようにきれいな数式の形で表示されます。

$2x^2 + 5xy + 3y^2$
$(x+y)(2x+3y)$

みやすいですね。

SymPyで式の展開と因数分解

Sympyで式の展開と因数分解をする方法を紹介しました。

今回、ご紹介したコードを整理しておきます。

import sympy

#xとyを文字として定義する
x = sympy.Symbol('x')
y = sympy.Symbol('y')

#多項式Pを定義して表示する
P = 2*x**2 + 5*x*y + 3*y**2
print(P)

#Pを因数分解して、Qと置き、表示する
Q = sympy.factor(P)
print(Q)

#Qを展開して表示する
print(sympy.expand(Q))

#PとQをLaTeX表示する
display(P)
display(Q)

はい、ご覧いただき、ありがとうございます！

様々な式に対して、因数分解できるか検証することもできますね！