- 表紙
- まとめ
- 具体例
数学のまとめ
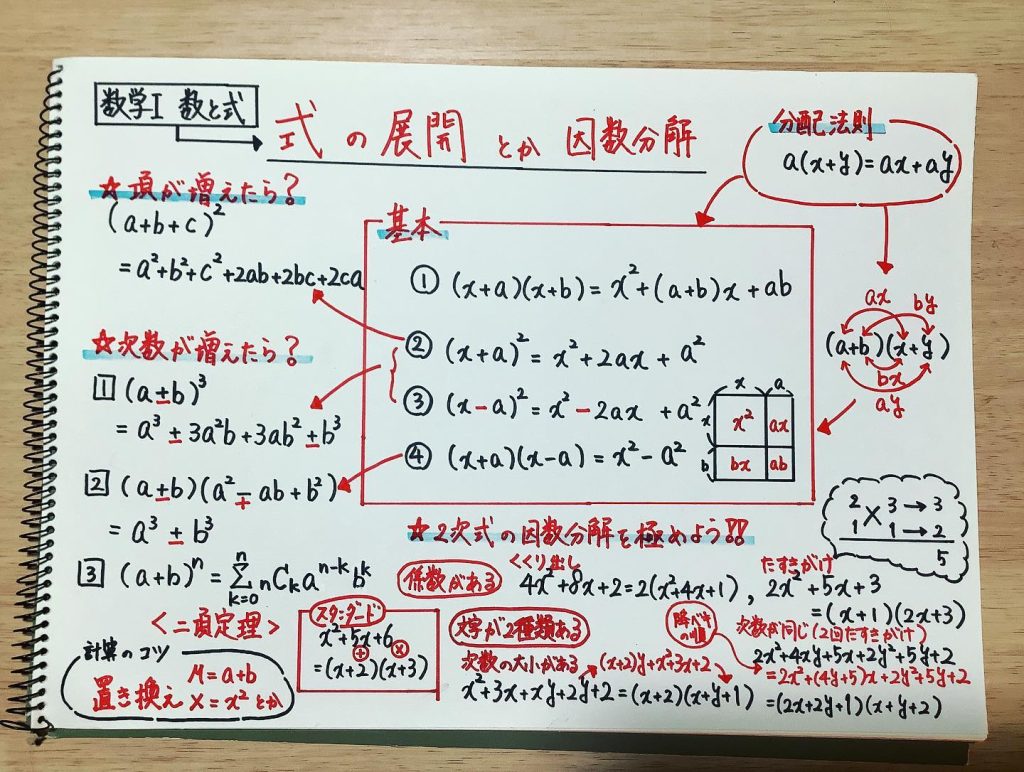
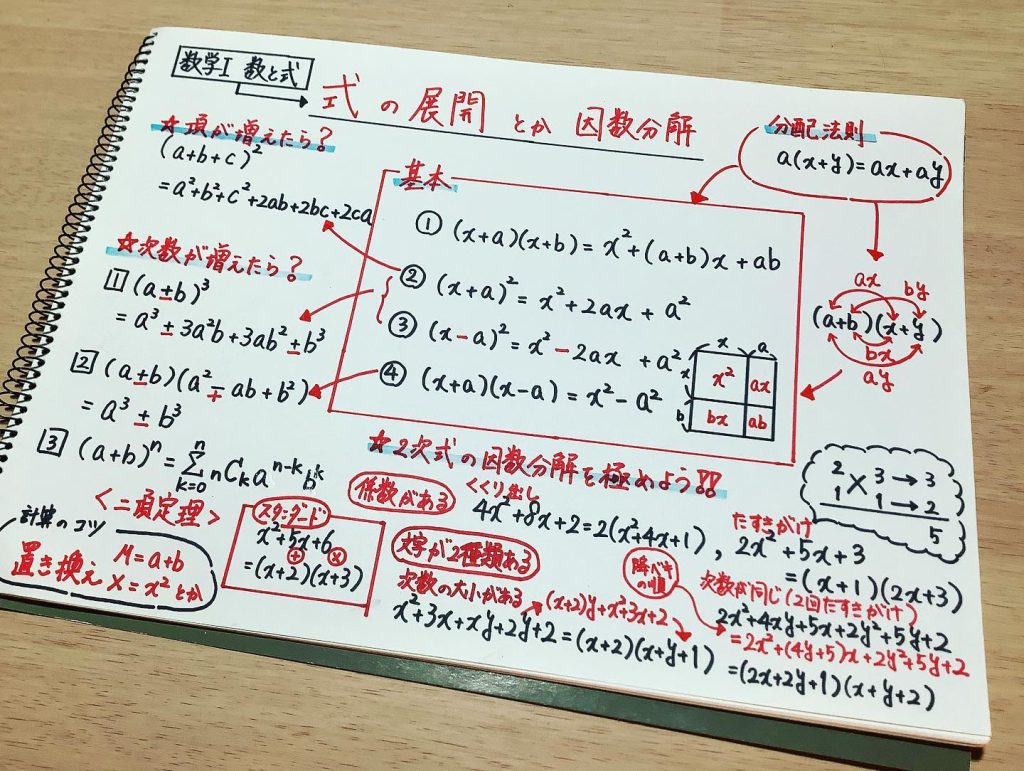
「式の展開」とは
多項式の積を単項式の和で表すこと。
分配法則
$a(x+y) = ax + ay$
が成り立つとする.
A. 乗法公式（２次式の展開）
- $(x+a)(x+b)$ $=x^2 + (a+b)x + ab$
- $(a\pm b)^2 = x^2 \pm 2ax + a^2$
- $(x+a)(x-a) = x^2-a^2$
B. 乗法公式（３次式の展開）
- $(x \pm a)^3$ $=x^3 \pm 3ax^2 + 3a^2x \pm a^3$
- $(x \pm a)(x^2 \mp ax + a^2)$ $=x^3 \pm a^3$
C. 展開公式（n次式の展開）
- $\displaystyle (x+a)^n = \sum_{k=0}^{n} {}_{n}\mathrm{C}_{k} x^{n-k} a^k$【二項定理】
- $(x - a)(x^{n-1} +ax^{n-2} +\cdots +a^{n-2}x+a^{n-1})$ $=x^n-a^n$
- $(x + a)(x^{n-1} -ax^{n-2} -\cdots -a^{n-2}x+a^{n-1})$ $=x^n+a^n$ 【 $n$ が奇数のときのみ】
ポイント解説
基礎
分配法則を基本として, 交換法則と結合法則から各公式が成り立つ。
A
面積としての意味がある。
3変数
$(x+y+z)^2=$ $x^2+y^2+z^2 +2xy+2yz+2zx$
B
体積としての意味がある。
C
(3) $n$ が偶数のときには不成立。
発展
いくつかの条件のもと任意の関数 $f(x)$ を展開できる（テイラー展開）：
$$f(x) = \sum_{n=0}^{\infty} \frac{f^{(n)}(0)}{n!}x^m$$
式の展開の具体例
関連事項
オリガミ（折り紙）で式の展開！
式の展開の知識をオリガミ（折り紙）で体験します。 応用力を磨きたい人にオススメです！ 高校数学の単元学習、普段の勉強を楽しく取り組みたい人にもオススメです。 目次…
ますレッスン教室 
オリガミ（折り紙）で3乗の立方公式！
式の展開と因数分解の３乗の計算の知識をオリガミ（折り紙）で体験します。 応用力を磨きたい人にオススメです！ 高校数学の単元学習、普段の勉強を楽しく取り組みたい人…
【Python】式の展開と因数分解をする方法（たすきがけ）
プログラミングで「たすきがけ」をしましょう。 Pythonで、「式の展開」をする方法と「因数分解」をする方法を紹介します。 Pythonって何？私にも使えるの？って方は、次…
導出
①$a(x+y)$ の展開
数の計算において，次のような分配法則はいつでも成り立つ。
$8 \times (10 + 2) = 8 \times 10 + 8\times2$
文字式の計算でも「分配法則」が必ず成り立つものと要請します。$$a(x+y) = ax + ay$$
②$(a+b)x$ の展開
分配法則 $a(x+y) = ax + ay$ と交換法則 $ax = xa$ を仮定する。
左辺から右辺を導く：
$(a+b)x$
$= x(a+b)$
$= xa + xb$
$= ax + bx$
よって，次が成立する：
$$(a+b)x = ax + bx$$
③$(x+a)(x+b)$ の展開
$a(x+y) = ax + ay$ と $(a+b)x = ax + bx$ を利用して，左辺から右辺を導く：
$(x+a)(x+b)$
$=(x+a)x + (x+a)b$
$= x^2 + ax + xb + ab$
$= x^2 + ax + bx + ab$
$= x^2 + (a+b)x + ab$
よって，次が成立する：
$$(x+a)(x+b) = x^2 + (a+b)x + ab$$
④$(x+a)^2$ の展開
③の式を利用して，左辺から右辺を導く：
$(x + a)^2$
$= (x + a)(x + a)$
$= x^2 + (a+a)x + a\cdot a$
$= x^2 + 2ax + a^2$
よって，次が成立する：
$$(x+a)^2 = x^2 + 2ax + a^2$$
⑤$(x-a)^2$ の展開
④の式を利用して，左辺から右辺を導く：
$(x - a)^2$
$= (x + (-a))^2$
$= x^2 + 2 \times (-a)x + (-a)^2$
$= x^2 - 2ax + a^2$
よって，次が成立する：
$$(x-a)^2 = x^2 - 2ax + a^2$$
⑥$(x+a)(x-a)$ の展開
③の式を利用して，左辺から右辺を導く：
$(x+a)(x-a)$
$= (x+a)(x+(-a))$
$= x^2 + (a + (-a))x + a \cdot (-a)$
$= x^2 + 0x -a^2$
$= x^2 -a^2$
よって，次が成立する：
$$(x+a)(x-a) = x^2 - a^2$$
