楕円の半径や離心率をパラメータとして、楕円のグラフをPythonで描くコードを紹介します。
楕円のPythonコード
半径から楕円を導くコード
$a>0$, $b>0$ であるとき, $\displaystyle \frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ の方程式は楕円を表します。$a$ が横軸方向の半径で, $b$ が縦軸方向の半径になります。
import matplotlib.pyplot as plt
import numpy as np
# 長軸と短軸の長さ
a = 2
b = 1
# パラメータを生成
theta = np.linspace(0, 2 * np.pi, 1000)
# 楕円の座標計算
x = a * np.cos(theta)
y = b * np.sin(theta)
# 楕円を描画
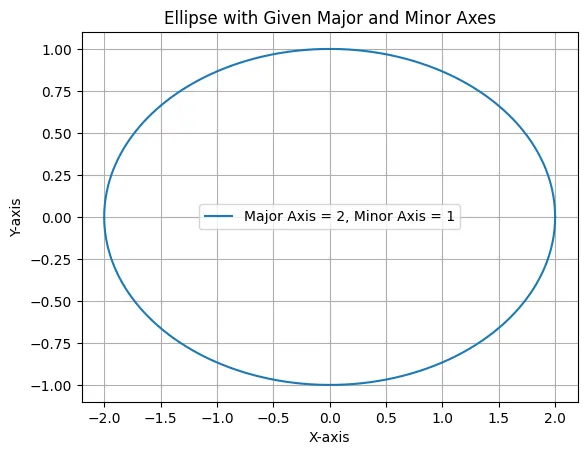
plt.plot(x, y, label=f'Major Axis = {a}, Minor Axis = {b}')
plt.title('Ellipse with Given Major and Minor Axes')
plt.xlabel('X-axis')
plt.ylabel('Y-axis')
plt.legend()
plt.grid(True)
plt.show()半径から楕円を導いた結果
離心率から楕円を導くコード
$a>b$ のときを考えます(横に長い楕円)。
このとき、離心率 $e<1$ と、上の $a$, $b$ の関係には $\displaystyle e = \frac{\sqrt{a^2- b^2}}{a}$ という関係があります。
これを $b$ について解けば $b = a(1-e^2)$ なので, $a$ と $e$ から楕円を決定することができます。
また、$a<b$ のとき(縦方向に長い楕円)では、$b$ と $e$ から, $a =b(1-e^2)$ を導くことができます。必要に応じて下のコードを書き換えてください。
import matplotlib.pyplot as plt
import numpy as np
# 離心率
eccentricity = 0.8
# 楕円のパラメータ
a = 1 # 長軸の半径
b = a * np.sqrt(1 - eccentricity**2) # 短軸の半径
# パラメータを生成
theta = np.linspace(0, 2 * np.pi, 100)
# 楕円の座標計算
x = a * np.cos(theta)
y = b * np.sin(theta)
# 楕円を描画
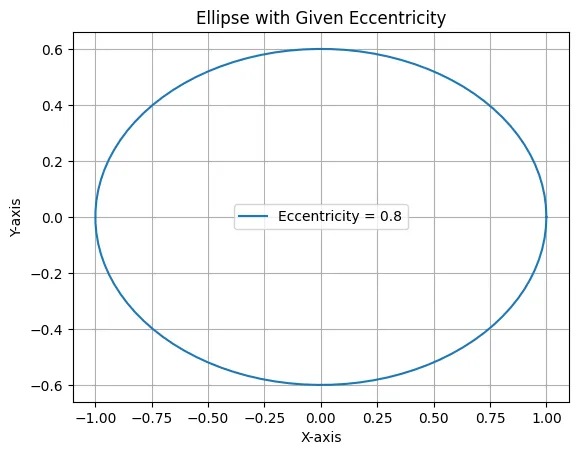
plt.plot(x, y, label=f'Eccentricity = {eccentricity}')
plt.title('Ellipse with Given Eccentricity')
plt.xlabel('X-axis')
plt.ylabel('Y-axis')
plt.legend()
plt.grid(True)
plt.show()離心率から楕円を導いた結果



