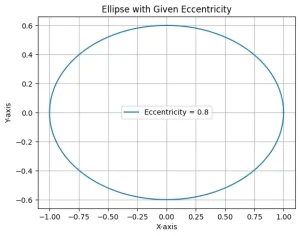
楕円の基本事項を整理します。
楕円の方程式
中心が原点である楕円の方程式は:
$$\displaystyle \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1.$$
- 定数 $a$:楕円の横軸方向の半径
- 定数 $b$:楕円の縦軸方向の半径
楕円の方程式
楕円の定義
数学的に、楕円の定義は次のように設定されています。
楕円は, 2点からの距離の和が一定の点の軌跡である.
楕円の方程式
まず、楕円の方程式と、その導出を説明します。
楕円の方程式
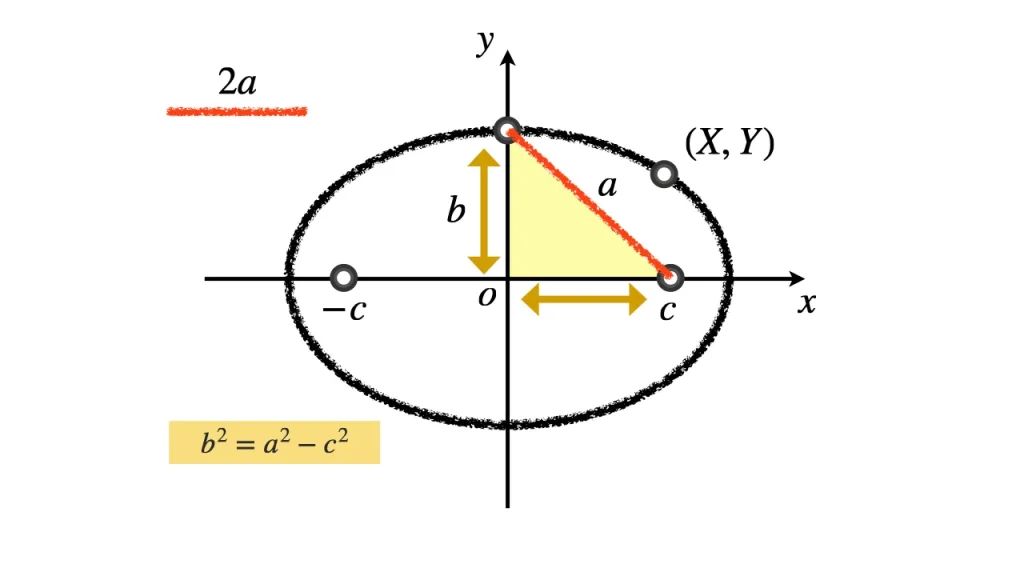
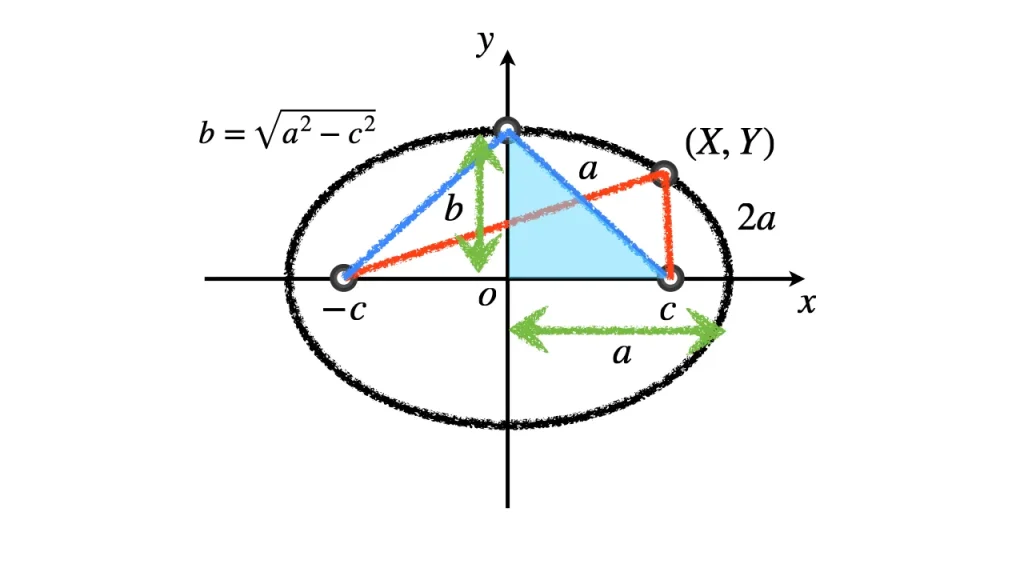
$a>0$ とする. 焦点が $x$ 軸上の $(c, 0)$, $ (-c, 0)$ であり, 焦点からの距離の和が $2a$ である点の軌跡は:
$$\displaystyle \frac{x^2}{a^2} + \frac{y^2}{a^2-c^2} = 1.$$
- 定数 $a$:楕円の横軸方向の半径に対応
- $\sqrt{a^2-c^2}$ は楕円の縦軸方向の半径に対応

楕円の方程式の成り立ち
楕円の方程式を導出しましょう。
証明すること→ 楕円の定義をもとに, 楕円の方程式を導出する.
証明.
楕円の定義を確認する
楕円は2つの点からの距離の和が一定の点の軌跡であった.
2つの点を $\mathrm{F}$ と $\mathrm{F'}$ とし, 距離の和を $2a$ とすれば, 動点 $\mathrm{P}$ の軌跡は次の通りである..
$$\displaystyle \mathrm{PF} + \mathrm{PF'} = 2a.$$
座標を設定する
焦点の座標を $\mathrm{F}(c, 0), \ \mathrm{F'}(-c, 0)$ とする.
また, 動点 $\mathrm{P}$ の座標を $(x,y)$ とする.
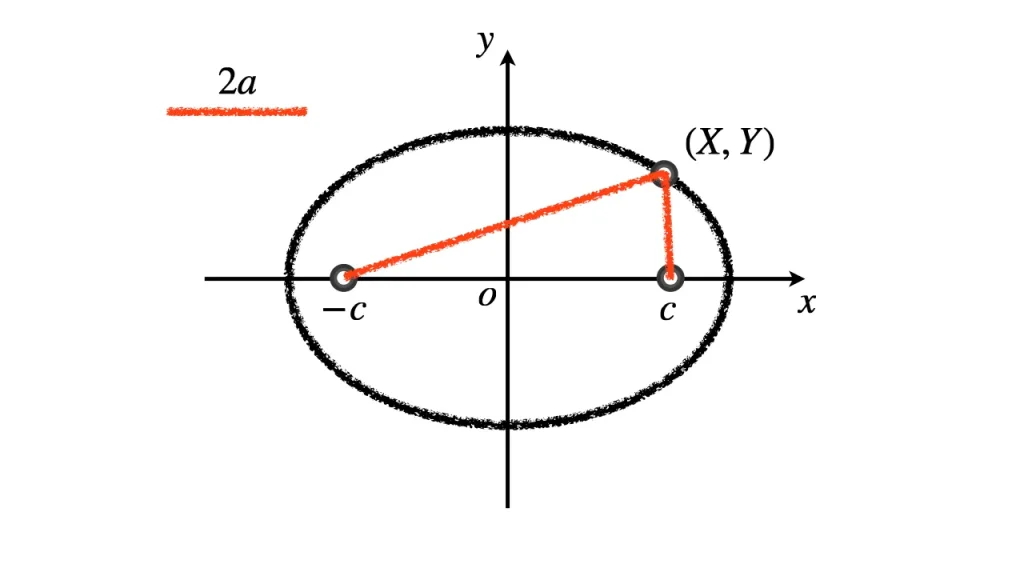
条件から立式する
定義式を座標を表す文字で書き換え, 立式しましょう.
まず, $\mathrm{PF}$ と $\mathrm{PF'}$ は次のようになる.
$\displaystyle \mathrm{PF} = \sqrt{(x-c)^2 + y^2}$
$\displaystyle \mathrm{PF'} = \sqrt{(x-(-c))^2 + y^2}$
これらを楕円の定義式に代入すれば, 次を得る:
$$\sqrt{(x-c)^2 + y^2} + \sqrt{(x-(-c))^2 + y^2} = 2a.$$
計算して簡単な数式にする
この式を計算する;
第2項目を右辺に移行し, 両辺を2乗する;
$\sqrt{(x-c)^2 + y^2} = 2a - \sqrt{(x-(-c))^2 + y^2}$
$(x-c)^2 + y^2 = 4a^2 - 4a \sqrt{(x+c)^2 + y^2} + (x+c)^2 + y^2$
もう一度, 2乗すれば, 平方根がなくなる形に変えたのち, 2乗して計算する;
$a \sqrt{(x+c)^2 + y^2} = a^2 + cx$
$(a^2 - c^2)x^2 + a^2y^2 = a^2(a^2 - c^2)$.
長軸半径を見つける
動点 $\mathrm{P}$ と $\mathrm{P'}$ が最も遠くなるときは, 2つとも $x$ 軸上にあるときである.
このときの距離は $2a$ である.
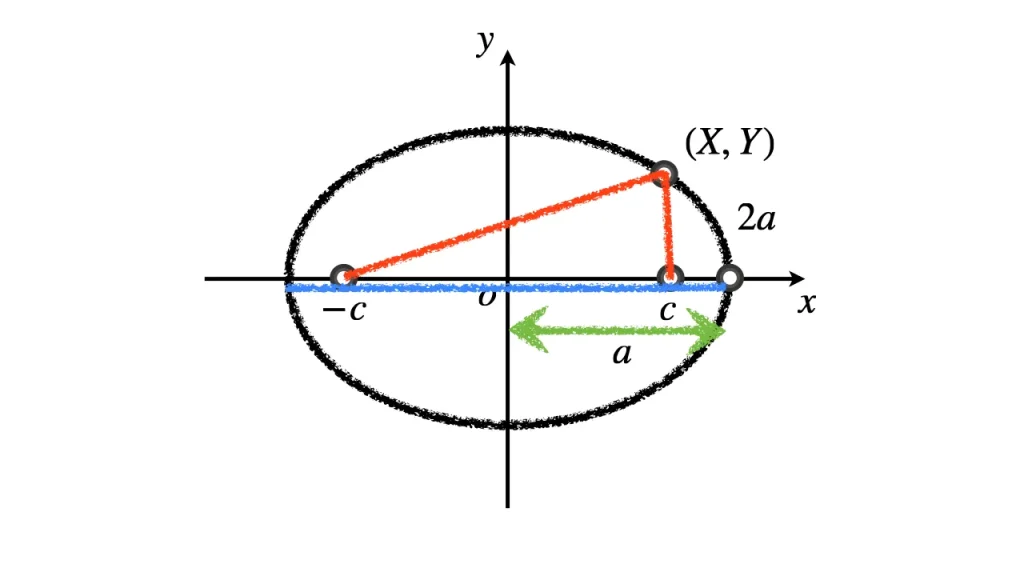
ゆえに, $a$ は楕円の長軸方向の半径の長さと一致する.
短軸半径を見つける
動点 $\mathrm{P}$ と $\mathrm{P'}$ が最も近くなるときは, 2つとも $y$ 軸上にあるときである.
図を見れば, 三平方の定理より, $\sqrt{a^2 - c^2}$ は, その距離の半分に一致する.

ゆえに, 短軸半径の $b = \sqrt{a^2 - c^2}$ が楕円の短軸方向の半径の長さと一致する.
楕円の方程式を完成させる
楕円の定義式から, 次の式を得ていた.
$$(a^2 - c^2)x^2 + a^2y^2 = a^2(a^2 - c^2)$$
$b^2 = a^2 - c^2$ と置く.
$$b^2 x^2 + a^2y^2 = a^2b^2$$
また, 図より $b>0$ と分かる. 両辺を $a^2b^2$ で割る.
$$\displaystyle \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1.$$
楕円の方程式が導けた. ■
楕円の方程式の性質
これまでは、定義に関する $a$ と $c$ を使って楕円の方程式を見てきました。
長軸と短軸の整理
ここでは、横軸方向の半径 $a$, 縦軸方向の半径 $b$ から出発して楕円の方程式を整理します。
① $a>b$ のとき
横方向に長い楕円になる;
- 長軸半径: $a$, 短軸半径: $b$
- 焦点の座標: $(\sqrt{a^2 - b^2}, \ 0)$, $(-\sqrt{a^2 - b^2}, \ 0)$
② $a<b$ のとき
縦方向に長い楕円になる;
- 短軸半径: $a$, 長軸半径: $b$
- 焦点: $(0, \ \sqrt{b^2 - a^2})$, $(0, \ -\sqrt{b^2 - a^2})$
$a=b=1$ のときは真ん丸な「円」になる。
楕円の方程式と性質(まとめ)
以上で、次のことが分かりました。
楕円の方程式
中心が原点である楕円の方程式は:
$$\displaystyle \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1.$$
- 定数 $a$:楕円の横軸方向の半径
- 定数 $b$:楕円の縦軸方向の半径