- 表紙
- まとめ
- 理解
- 意味
- コード
数学のまとめノート
「楕円」とは
円を伸縮してできる曲線のこと。
定義
2点からの距離の和が一定の点の軌跡を楕円という.
A. 楕円の方程式
原点中心, 横半径 $a>0$, 縦半径 $b>0$ の楕円: $\displaystyle \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$.
B. 楕円の接線方程式
楕円上の $(x_0, y_0)$ を通る接線の方程式: $\displaystyle \frac{x_0}{a^2}x + \frac{y_0}{b^2}y = 1$
離心率
楕円の離心率 $e$ は, (焦点間の距離)/(長軸方向の直径)で与えられる. $0<e<1$ である.
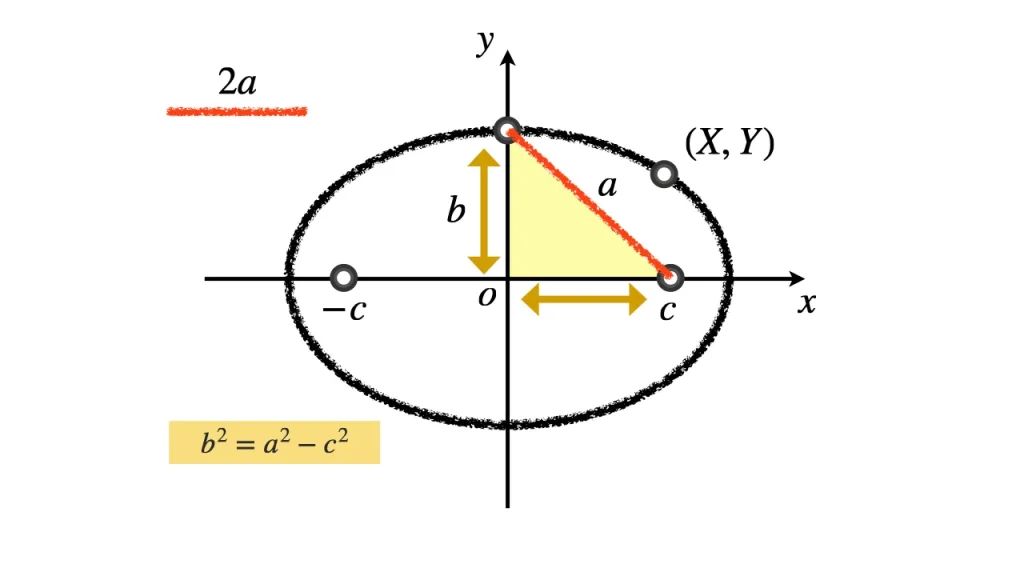
C. 横長の楕円 $(a>b)$
- 焦点からの距離の和: $2a$
- 焦点: $(c, 0)$, $(-c,0)$
- $c^2 = a^2 - b^2$
- 離心率: $e=c/a$
- 焦点 $(ae, 0)$, 準線: $x=a/e$
D. 縦長の楕円 $(a<b)$
- 焦点からの距離の和: $2b$
- 焦点: $(0, c)$, $(0, -c)$
- $c^2 = b^2 - a^2$
- 離心率: $e=c/b$
- 焦点 $(0, be)$, 準線: $y=b/e$
ポイント解説
定義
距離の和を $2a$, 焦点を $\mathrm{F}$ と $\mathrm{F}'$, 動点を $\mathrm{P}$ とすると, $\mathrm{PF} + \mathrm{PF'} = 2a$.
A・C
横方向に長い楕円の図:
C・D
$a=b$ のときは円になる.
離心率
(焦点からの距離)と(準線からの距離の比) が $e:1$ になる点の軌跡は楕円である。
イメージ
楕円は自然に現れる。


楕円の数式
楕円の基本事項を整理します。
楕円の方程式
中心が原点である楕円の方程式は:
$$\displaystyle \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1.$$
- 定数 $a$:楕円の横軸方向の半径
- 定数 $b$:楕円の縦軸方向の半径

楕円の方程式
楕円の定義
数学的に、楕円の定義は次のように設定されています。
楕円は, 2点からの距離の和が一定の点の軌跡である.
楕円の方程式
まず、楕円の方程式と、その導出を説明します。
楕円の方程式
$a>0$ とする. 焦点が $x$ 軸上の $(c, 0)$, $ (-c, 0)$ であり, 焦点からの距離の和が $2a$ である点の軌跡は:
$$\displaystyle \frac{x^2}{a^2} + \frac{y^2}{a^2-c^2} = 1.$$
- 定数 $a$:楕円の横軸方向の半径に対応
- $\sqrt{a^2-c^2}$ は楕円の縦軸方向の半径に対応

楕円の方程式の成り立ち
楕円の方程式を導出しましょう。
証明すること→ 楕円の定義をもとに, 楕円の方程式を導出する.
証明.
楕円の定義を確認する
楕円は2つの点からの距離の和が一定の点の軌跡であった.
2つの点を $\mathrm{F}$ と $\mathrm{F'}$ とし, 距離の和を $2a$ とすれば, 動点 $\mathrm{P}$ の軌跡は次の通りである..
$$\displaystyle \mathrm{PF} + \mathrm{PF'} = 2a.$$
座標を設定する
焦点の座標を $\mathrm{F}(c, 0), \ \mathrm{F'}(-c, 0)$ とする.
また, 動点 $\mathrm{P}$ の座標を $(x,y)$ とする.
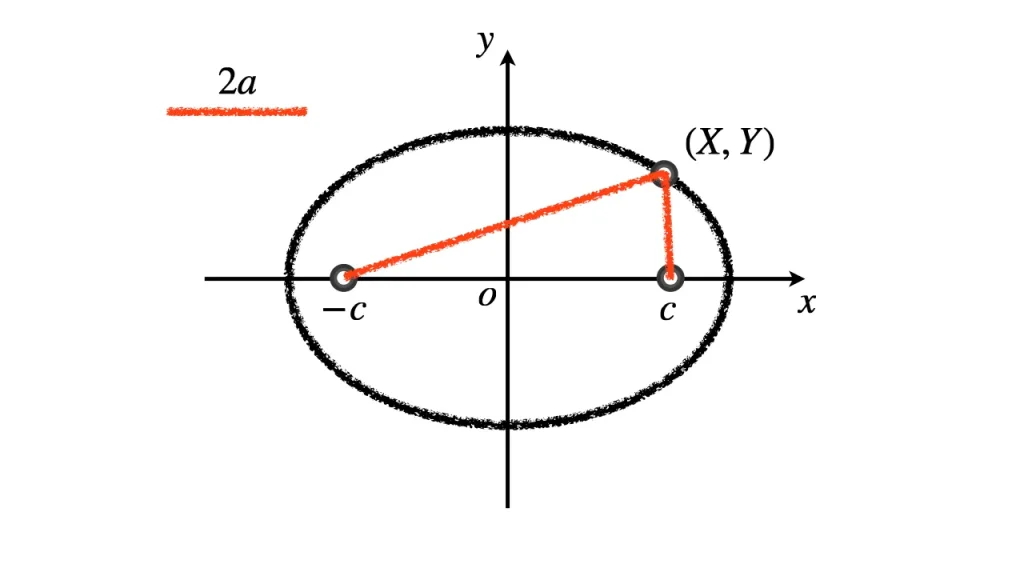
条件から立式する
定義式を座標を表す文字で書き換え, 立式しましょう.
まず, $\mathrm{PF}$ と $\mathrm{PF'}$ は次のようになる.
$\displaystyle \mathrm{PF} = \sqrt{(x-c)^2 + y^2}$
$\displaystyle \mathrm{PF'} = \sqrt{(x-(-c))^2 + y^2}$
これらを楕円の定義式に代入すれば, 次を得る:
$$\sqrt{(x-c)^2 + y^2} + \sqrt{(x-(-c))^2 + y^2} = 2a.$$
計算して簡単な数式にする
この式を計算する;
第2項目を右辺に移行し, 両辺を2乗する;
$\sqrt{(x-c)^2 + y^2} = 2a - \sqrt{(x-(-c))^2 + y^2}$
$(x-c)^2 + y^2 = 4a^2 - 4a \sqrt{(x+c)^2 + y^2} + (x+c)^2 + y^2$
もう一度, 2乗すれば, 平方根がなくなる形に変えたのち, 2乗して計算する;
$a \sqrt{(x+c)^2 + y^2} = a^2 + cx$
$(a^2 - c^2)x^2 + a^2y^2 = a^2(a^2 - c^2)$.
長軸半径を見つける
動点 $\mathrm{P}$ と $\mathrm{P'}$ が最も遠くなるときは, 2つとも $x$ 軸上にあるときである.
このときの距離は $2a$ である.
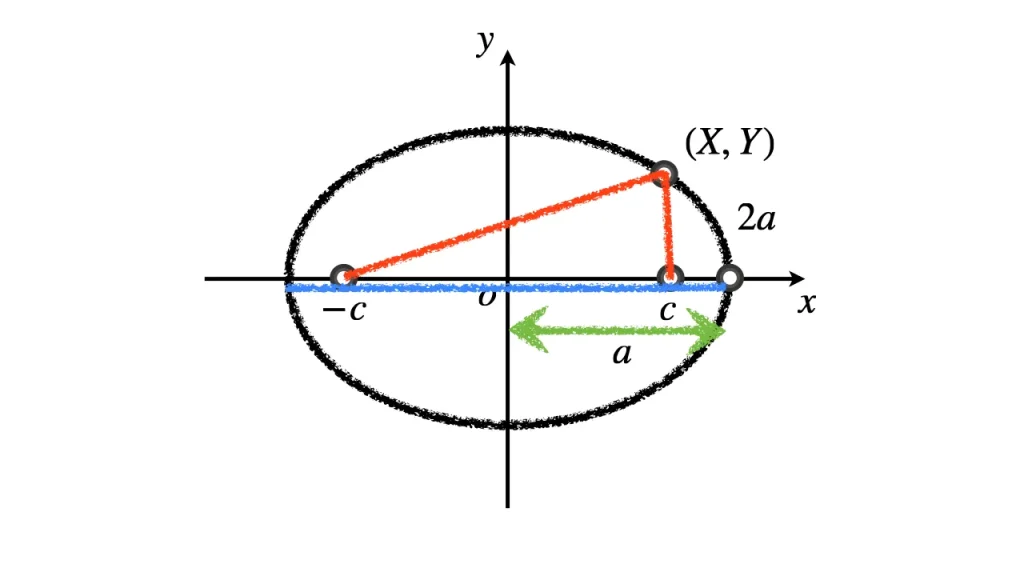
ゆえに, $a$ は楕円の長軸方向の半径の長さと一致する.
短軸半径を見つける
動点 $\mathrm{P}$ と $\mathrm{P'}$ が最も近くなるときは, 2つとも $y$ 軸上にあるときである.
図を見れば, 三平方の定理より, $\sqrt{a^2 - c^2}$ は, その距離の半分に一致する.

ゆえに, 短軸半径の $b = \sqrt{a^2 - c^2}$ が楕円の短軸方向の半径の長さと一致する.
楕円の方程式を完成させる
楕円の定義式から, 次の式を得ていた.
$$(a^2 - c^2)x^2 + a^2y^2 = a^2(a^2 - c^2)$$
$b^2 = a^2 - c^2$ と置く.
$$b^2 x^2 + a^2y^2 = a^2b^2$$
また, 図より $b>0$ と分かる. 両辺を $a^2b^2$ で割る.
$$\displaystyle \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1.$$
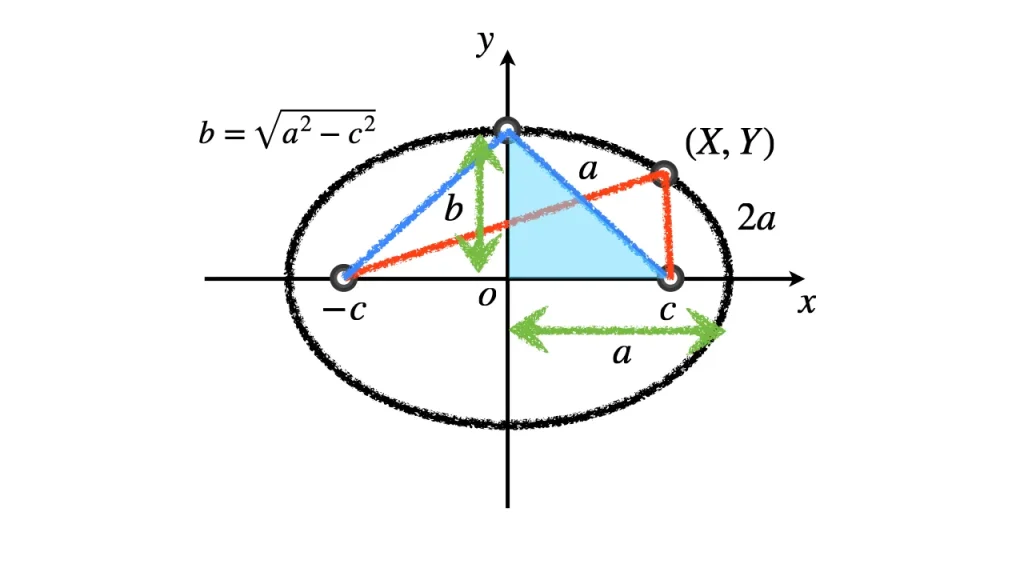
楕円の方程式が導けた. ■
楕円の方程式の性質
これまでは、定義に関する $a$ と $c$ を使って楕円の方程式を見てきました。
長軸と短軸の整理
ここでは、横軸方向の半径 $a$, 縦軸方向の半径 $b$ から出発して楕円の方程式を整理します。
① $a>b$ のとき
横方向に長い楕円になる;
- 長軸半径: $a$, 短軸半径: $b$
- 焦点の座標: $(\sqrt{a^2 - b^2}, \ 0)$, $(-\sqrt{a^2 - b^2}, \ 0)$
② $a<b$ のとき
縦方向に長い楕円になる;
- 短軸半径: $a$, 長軸半径: $b$
- 焦点: $(0, \ \sqrt{b^2 - a^2})$, $(0, \ -\sqrt{b^2 - a^2})$
$a=b=1$ のときは真ん丸な「円」になる。
楕円の方程式と性質(まとめ)
以上で、次のことが分かりました。
楕円の方程式
中心が原点である楕円の方程式は:
$$\displaystyle \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1.$$
- 定数 $a$:楕円の横軸方向の半径
- 定数 $b$:楕円の縦軸方向の半径

円との関係(伸縮)
楕円は、円をギュッとした形です。
これを数学的に解説します!
円の拡大縮小による楕円の導出
単位円 $x^2 + y^2 =1$ を $x$ 軸方向に $a$ 倍,$y$ 軸方向に $b$ 倍した図形の方程式は次と一致する:
$$\displaystyle \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$$
円を伸縮すると楕円
円を「ギュッとする」とは、伸縮させるという意味です。
今回のテーマ(問い)は、「円を伸縮させたら楕円になるらしい」というものです。
はじめに、円と楕円が何かを確認し、問いを確かめます。
楕円の方程式
まず、楕円が何かを明確にしておきましょう。
今回は、教科書に書いている次の方程式が楕円ということを基準にしたいと思います。
楕円の方程式
楕円の中心が原点であり, $x$ 軸方向の半径が $a>0$, $y$ 軸方向の半径が $b>0$ の楕円の方程式は次の通り:
$$\displaystyle \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1.$$

円を伸縮させた形
円は数学では $x^2+y^2=1$ で表せます。
伸縮させるとは、同じ倍率で拡大もしくは縮小させるという意味です。
数学的には、例えば、$(3, 1)$ という点を $(6, 1)$ にして、さらに $(2, 3)$ という点を $(4, 3)$ にするのは「$y$ 軸を基準に $x$ 軸方向に $2$ 倍に拡大した」と思うことができます。$1/2$ 倍だったら、縮小させたと思えます。
証明で確かめる
証明すること→単位円 $x^2 + y^2 =1$ を $x$ 軸方向に $a$ 倍, $y$ 軸方向に $b$ 倍した図形の方程式は次と一致する: $$\displaystyle \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$$
証明.単位円 $x^2 + b^2 =1$ を横方向と縦方向の両方に伸縮するという変形が, 楕円の方程式を導くことを示す.
横軸方向に伸縮させる
円を 「$x$ 軸方向に伸縮させる」ことを, $y$ 軸を基準に同じ比率($a>0$)で等倍すると定める.
つまり, 円周上の点 $(x,y)$ を $(ax, y)$ と変形する. 等倍されたあとの円周上の点の座標は $(ax, y)$ となる.
縦軸方向に伸縮させる
円を 「$y$ 軸方向に伸縮させる」ことを, $x$ 軸を基準に同じ比率($b>0$)で等倍すると定める.
つまり, 円周上の点 $(x,y)$ を $(x, by)$ と変形する. 等倍されたあとの円周上の点の座標は $(x, by)$ となる.
伸縮後の座標と方程式
円を $x$ 軸と$y$ 軸方向にそれぞれ伸縮したあとの点$(X,Y)$ の座標は $(ax, by)$ である.
$$(X,Y) = (ax, by)$$
$x = X/a$ と $y = Y/b$ を, 単位円の方程式 $(x^2 + y^2 = 1)$ に代入すると, 次の通り:
$$\displaystyle \left( \frac{X}{a} \right)^2 + \left( \frac{Y}{b} \right)^2 = 1$$
すなわち, 楕円の方程式である $\displaystyle \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$ を得る, ■
以上から、次のことを確かめることができました!
円の拡大縮小による楕円の導出
単位円 $x^2 + y^2 =1$ を $x$ 軸方向に $a$ 倍,$y$ 軸方向に $b$ 倍した図形の方程式は次と一致する:
$$\displaystyle \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$$
Pythonコード
楕円の半径や離心率をパラメータとして、楕円のグラフをPythonで描くコードを紹介します。
楕円のPythonコード
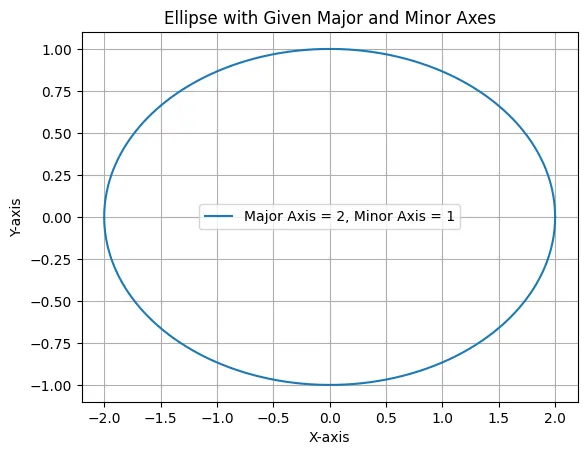
半径から楕円を導くコード
$a>0$, $b>0$ であるとき, $\displaystyle \frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ の方程式は楕円を表します。$a$ が横軸方向の半径で, $b$ が縦軸方向の半径になります。
import matplotlib.pyplot as plt
import numpy as np
# 長軸と短軸の長さ
a = 2
b = 1
# パラメータを生成
theta = np.linspace(0, 2 * np.pi, 1000)
# 楕円の座標計算
x = a * np.cos(theta)
y = b * np.sin(theta)
# 楕円を描画
plt.plot(x, y, label=f'Major Axis = {a}, Minor Axis = {b}')
plt.title('Ellipse with Given Major and Minor Axes')
plt.xlabel('X-axis')
plt.ylabel('Y-axis')
plt.legend()
plt.grid(True)
plt.show()半径から楕円を導いた結果
離心率から楕円を導くコード
$a>b$ のときを考えます(横に長い楕円)。
このとき、離心率 $e<1$ と、上の $a$, $b$ の関係には $\displaystyle e = \frac{\sqrt{a^2- b^2}}{a}$ という関係があります。
これを $b$ について解けば $b = a(1-e^2)$ なので, $a$ と $e$ から楕円を決定することができます。
また、$a<b$ のとき(縦方向に長い楕円)では、$b$ と $e$ から, $a =b(1-e^2)$ を導くことができます。必要に応じて下のコードを書き換えてください。
import matplotlib.pyplot as plt
import numpy as np
# 離心率
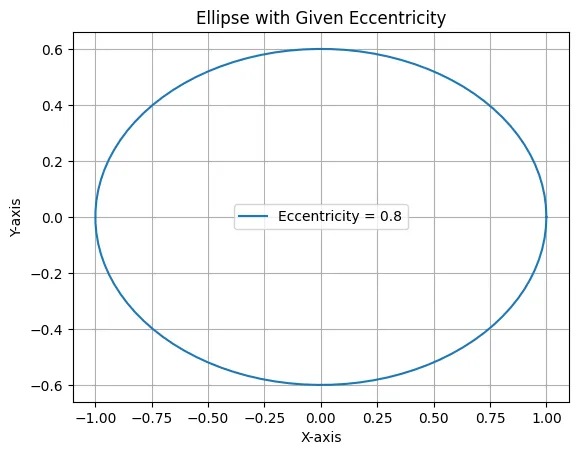
eccentricity = 0.8
# 楕円のパラメータ
a = 1 # 長軸の半径
b = a * np.sqrt(1 - eccentricity**2) # 短軸の半径
# パラメータを生成
theta = np.linspace(0, 2 * np.pi, 100)
# 楕円の座標計算
x = a * np.cos(theta)
y = b * np.sin(theta)
# 楕円を描画
plt.plot(x, y, label=f'Eccentricity = {eccentricity}')
plt.title('Ellipse with Given Eccentricity')
plt.xlabel('X-axis')
plt.ylabel('Y-axis')
plt.legend()
plt.grid(True)
plt.show()離心率から楕円を導いた結果