
ドラゴン曲線というフラクタル図形があります。
「アートで魅せる数学の世界(著:岡本健太郎)」という書籍で知って、Wikipediaの「ドラゴン曲線」のページで概要を知りました。
「アートで魅せる数学の世界」ではExcelでドラゴン曲線を作成していたので、今回はPythonで作成してみました。
ドラゴン曲線をPythonで作成
ドラゴン曲線のイラスト
ドラゴン曲線には、いくつかの種類があります。ここではヘイウェイ・ドラゴンを作成します。
ドラゴン曲線には「世代」という概念があります。定義のアルゴリズムの回数を1つ重ねることを世代でカウントしています。
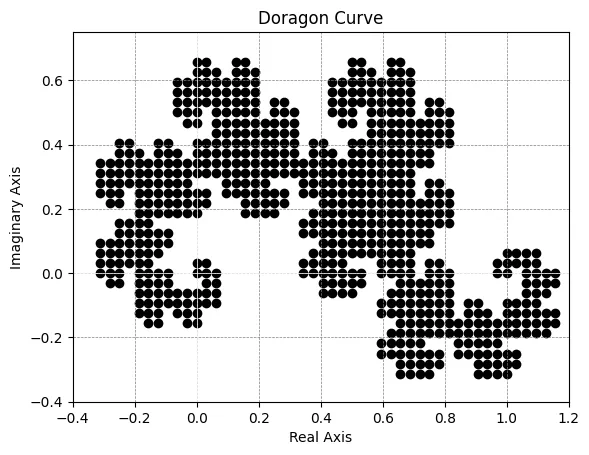
第11世代のヘイウェイ・ドラゴンをPythonで作成したものです。
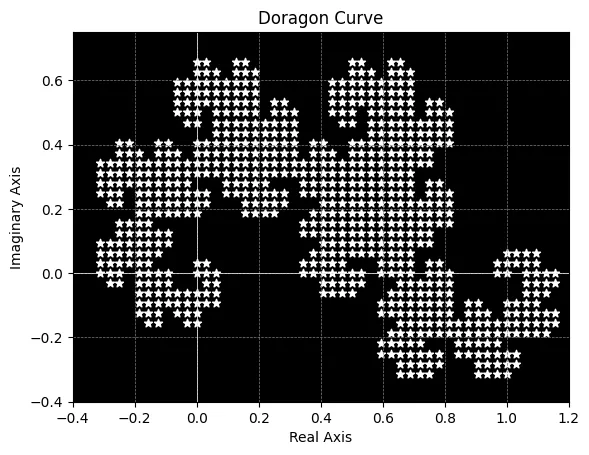
気まぐれで白黒反転させてみました。
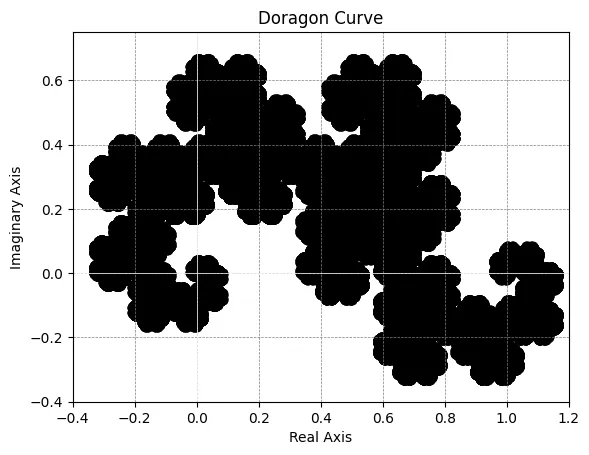
世代を上げて、第21世代のヘイウェイ・ドラゴンを作成しました。
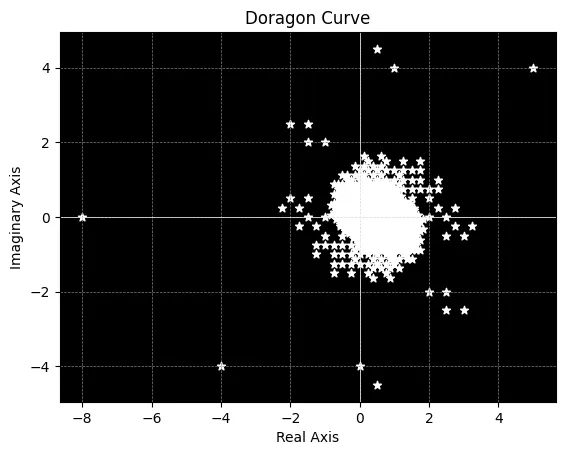
あと、ツインドラゴンという曲線を作成していたときに、偶然できた図を掲載します。
綺麗な銀河系みたいな図ができました🐲🐲。
ドラゴン曲線のPythonコード
紹介してきたドラゴン曲線のコードを掲載します。
「#世代」のgenerationの値を変えることで、より複雑なヘイウェイ・ドラゴンを作成することができます。
import matplotlib.pyplot as plt
import numpy as np
#関数の定義
def doragon1(z1):
f1 = (1+1j)/2*z1
return f1
def doragon2(z2):
f2 = 1- (1-1j)/2*z2
return f2
# 世代
generation = 11
# 初期集合
doragon = {0, 1}
for i in range(generation-1):
new_pts = set()
# 反復計算
for z in doragon:
z1 = doragon1(z)
z2 = doragon2(z)
new_pts.add(z1)
new_pts.add(z2)
doragon = doragon.union(new_pts)
print(doragon)
# 実部と虚部の取得
real_values = [np.real(z) for z in doragon]
imag_values = [np.imag(z) for z in doragon]
# 複素数平面への図示
fig, ax = plt.subplots()
ax.scatter(real_values, imag_values, color='white', marker='*')
ax.axhline(0, color='white', linewidth=0.5)
ax.axvline(0, color='white', linewidth=0.5)
# 背景色を白に設定
fig.patch.set_facecolor('white')
ax.set_facecolor('black')
plt.grid(color = 'gray', linestyle = '--', linewidth = 0.5)
plt.xlabel('Real Axis')
plt.ylabel('Imaginary Axis')
plt.title('Doragon Curve')
plt.xlim([-0.4, 1.2]) # 横軸の範囲を設定
plt.ylim([-0.4, 0.75]) # 縦軸の範囲を設定
plt.show()

