- 表紙
- まとめ
- センス
- 絵描き
- すうがく

ベジェ曲線のイメージと数学を勉強しましょう!
まとめノート
ベジェ曲線とは
直感的に描きやすく、コンピュータやイラストソフトで滑らかに描ける曲線のこと。
制御点
$n+1$ 個の点 $\mathbf{P}_0$, $\mathbf{P}_1$, $\ldots$ , $\mathbf{P}_n$ をとる.
A. $n$ 次ベジェ曲線
$t \in [0, \ 1]$ のときの $\mathbf{P}(t)$ が描く軌跡を $n$ 次ベジェ曲線という.
$\displaystyle \mathbf{P}(t) = \sum_{k=0}^{n} {}_n \mathrm{C}_k (1-t)^{n-k} \ t^k \ \mathbf{P}_k$
B. ド・カステリョのアルゴリズム
$t \in [0, \ 1]$ とする. 下記の漸化式で定まる $\mathbf{P}(t) = \mathbf{P}_0^n(t)$ は $n$ 次ベジェ曲線と一致する. ただし, $k \in \{ 0,\ \cdots , \ n -i \}$ とする.
$$\mathbf{P}_k^i(t) = \left\{ \begin{array}{cl} \mathbf{P}_k, & i =0 \\
(1-t)\mathbf{P}_k^{i-1}(t) + t\mathbf{P}_{k+1}^{i-1}(t), & i \in \{ 1,\ \cdots , \ n\}
\end{array}\right.$$
C. ベジェ曲線の性質
- ハンドルはアンカーポイントの接線である
- アンカーポイント以外の制御点はベジェ曲線上の点ではない
- $2$次ベジェ曲線は, アンカーポイントを結ぶ線分を描く
ポイント解説
制御点
$\mathbf{P}_0$ と $\mathbf{P}_1$ は曲線の端点を決める
アンカーポイント
という. $\mathbf{P}_0\mathbf{P}_1$と $\mathbf{P}_n\mathbf{P}_{n-1}$ は, 端点での曲線の接線方向と曲がり具合を決める
ハンドル
という.

B
制御点の間を $(1-t):t$ に内分する点を繰り返し取るアルゴリズム:

C
拡大縮小に最適(
ベクター形式
)

モチベーション
考えてみよう?!
パソコンでイラストを描いたものを拡大・縮小するとボヤけるときがあります。
しかし、ベジェ曲線の図は、拡大・縮小してもボヤけません。
なぜでしょうか?
①$a(x+y)$ の展開
数の計算において,次のような分配法則はいつでも成り立つ。
$8 \times (10 + 2) = 8 \times 10 + 8\times2$
文字式の計算でも「分配法則」が必ず成り立つものと要請します。$$a(x+y) = ax + ay$$
②$(a+b)x$ の展開
分配法則 $a(x+y) = ax + ay$ と交換法則 $ax = xa$ を仮定する。
左辺から右辺を導く:
$(a+b)x$
$= x(a+b)$
$= xa + xb$
$= ax + bx$
よって,次が成立する:
$$(a+b)x = ax + bx$$
③$(x+a)(x+b)$ の展開
$a(x+y) = ax + ay$ と $(a+b)x = ax + bx$ を利用して,左辺から右辺を導く:
$(x+a)(x+b)$
$=(x+a)x + (x+a)b$
$= x^2 + ax + xb + ab$
$= x^2 + ax + bx + ab$
$= x^2 + (a+b)x + ab$
よって,次が成立する:
$$(x+a)(x+b) = x^2 + (a+b)x + ab$$
④$(x+a)^2$ の展開
③の式を利用して,左辺から右辺を導く:
$(x + a)^2$
$= (x + a)(x + a)$
$= x^2 + (a+a)x + a\cdot a$
$= x^2 + 2ax + a^2$
よって,次が成立する:
$$(x+a)^2 = x^2 + 2ax + a^2$$
そういうものだから。
そうなんですけど、もう少し考えてみよう!
曲線を決める材料が少ないから。
正解!
おめでとう!
パチパチ!
きれいに曲線ができるから。
ざんねん!
ボヤけたところを自動的に修復してくれるから。
ざんねん!
関連リンクとイメージ集



お絵描き
ベジェ曲線は、パソコンで綺麗な(滑らかな)曲線を(簡単に)描くために利用されます、
ベクター形式と呼ばれ、デザインや設計と相性がよい曲線です。

ベジェ曲線を使えばこんな図が簡単に描けます!
この曲線の理論は、フランス自動車メーカーのド・カステリョとピエール・ベジェが独立に考案しました。1900年の真ん中ごろのお話です。
ベジェ曲線のパーツ
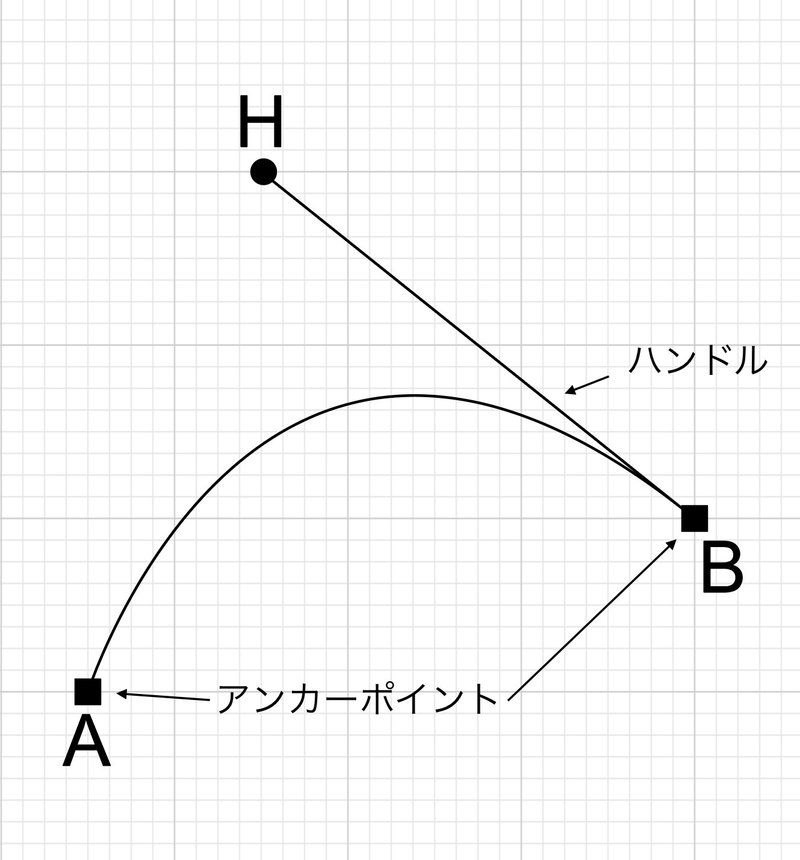
ベジェ曲線はアンカーポイントとハンドルを指定することで描くことができます。
点AとBがアンカーポイントと呼ばれる点です。
これらが描きたい曲線の両端の点になります。
線分BHがハンドルと呼ばれる、曲線の曲がり具合と曲がる向きを調整するものです。
ハンドルは、点Aの方にも指定して、より複雑な曲線を作ることもできます。
ちなみに、Aと、B、Hの点をすべてあわせて制御点といいます。
ベジェ曲線の描き方
2つのアンカーポイントで曲線の両端点を指定して、いくつかのハンドルを指定することで,曲線の曲がり具合を調整します。
直線の描き方
アンカーポイントの点①②を2つ打つだけで、線分が描けます。
綺麗な曲線の描き方
アンカーポイントの点①②を2つ打ち、②の場所でハンドルを指定しました。
これだけで様々な曲線が描けます。
少し複雑になった、この曲線を2次のベジェ曲線といいます。
さらに滑らかな曲線の描き方
アンカーポイントの点①②の両方でハンドルを作ります。
これで、かなり複雑な曲線も描けます。
この曲線を3次のベジェ曲線といいます。
すうがく
ベジェ曲線が描かれる仕組み(アルゴリズム)を紹介します。
ベジェ曲線の数式
ベジェ曲線の定義
定義
平面内の点 $\mathbf{P}_0$, $\mathbf{P}_1$, $\ldots$ , $\mathbf{P}_n$ と $0 \leqq t \leqq 1$ について,次の式で表される曲線を $n$次ベジェ曲線という。
$$\displaystyle \mathbf{P}(t) = \sum_{k=0}^{n} {}_n \mathrm{C}_k (1-t)^{n-k}t^k \mathbf{P}_k$$
3次ベジェ曲線で説明をします。4点 $\mathbf{P}_0$, $\mathbf{P}_1$, $\mathbf{P}_2$, $\mathbf{P}_3$ が制御点に該当します。
ドカステリョのアルゴリズムを数式で表して、ベジェ曲線の方程式を求めます。
ド・カステリョのアルゴリズム
まず、ベジェ曲線が描かれるアルゴリズムの直感的な理解をします。
①制御点の順番を決める
次のベジェ曲線を考えます。アンカーポイントは $\mathbf{P}_0$ と $\mathbf{P}_3$ が該当します。

制御点の順番を $\mathbf{P}_0$→$\mathbf{P}_1$→$\mathbf{P}_{2}$→$\mathbf{P}_3$ とします。
②同じ比に内分する点の作図
隣り合う制御点を $m:n$ に内分する点を作図します。

今回は、3つの点ができます。
③同じ比に内分する点の作図
いまできた3点について,さらに隣り合う点同士を,また $m:n$ に内分する点を作図します。

今回は、2つの点ができます。
④同じ比に内分する点の作図
いまできた2点について,さらに隣り合う点同士を,また $m:n$ に内分する点を作図します。

この作業を繰り返した結果、1点だけになりました。
この最後の点がベジェ曲線上の点と一致します。
⑤他の点も作図
他の比でも同じ作業をしていって、たくさん点を作ったら、その集まりがベジェ曲線になります。
$m:n = 1:0$ のとき、はじめのアンカーポイントの $\mathrm{P}_0$ です。
$m:n = 0:1$ のとき、ゴールのアンカーポイントの $\mathrm{P}_1$ です。
ベジェ曲線の数学の理解
先の直感的な作図に照らし合わせて、ベジェ曲線の定義式を作っていきましょう。
①図と式を対応させる
$\mathbf{P}_0$ と $\mathbf{P}_3$ がベジェ曲線の端点(アンカーポイント)になるべき点です。

イラストレータでは、線分 $\mathbf{P}_0 \mathbf{P}_1$ と $\mathbf{P}_3 \mathbf{P}_2$ がハンドルと対応する。
②制御点を結ぶ線分の内分点をつくる
$\mathbf{P}_0$→$\mathbf{P}_1$ と $\mathbf{P}_1$→$\mathbf{P}_2$, $\mathbf{P}_2$→$\mathbf{P}_3$ の間をそれぞれ $m: n = t : 1-t$ に内分する点を $\mathbf{P}_{1,0}(t)$, $\mathbf{P}_{1,1}(t)$,$\mathbf{P}_{1,2}(t)$ とします:
- $\mathbf{P}_{1,0}(t) = (1-t) \mathbf{P}_0 + t\mathbf{P}_1$
- $\mathbf{P}_{1,1}(t) = (1-t) \mathbf{P}_1 + t\mathbf{P}_2$
- $\mathbf{P}_{1,2} (t)= (1-t) \mathbf{P}_{2} + t\mathbf{P}_3$

③更に内分点をつくる
いまできた点について,$\mathbf{P}_{1,0}$→$\mathbf{P}_{1,1}$ と $\mathbf{P}_{1,1}$→$\mathbf{P}_{1,2}$ の間をそれぞれ,また $m: n = t : 1-t$ に内分する点を $\mathbf{P}_{2,0}(t), \mathbf{P}_{2,1}(t)$ とします:
- $\mathbf{P}_{2,0}(t) = (1-t) \mathbf{P}_{1,0} + t\mathbf{P}_{1,1}$
- $\mathbf{P}_{2,1}(t) = (1-t) \mathbf{P}_{1,1} + t\mathbf{P}_{1,2}$

④もういちど繰り返す
さらに,点$\mathbf{P}_{2,0}(t)$ → $\mathbf{P}_{2,1}(t)$ の間を結んで,また,$m: n = t : 1-t$ に内分する点 $\mathbf{P}(t)$ を決める:
- $\mathbf{P}(t) = (1-t) \mathbf{P}_{2,0} + t\mathbf{P}_{2,1}$

⑤式を整理する
点 $\mathbf{P}_{2,0}(t)$ と $\mathbf{P}_{2,1}(t)$ は,今までの式を組み合わせると,初めの制御点 $\mathbf{P}_0$, $\mathbf{P}_1$, $\mathbf{P}_2$, $\mathbf{P}_3$ で表すことができる。$\mathbf{P}(t)$ をはじめの制御点で表すと,
$\mathbf{P}(t) = (1-t) \mathbf{P}_{2,0} + t\mathbf{P}_{2,1}$
$= (1-t)^3 \mathbf{P}_0$ $+3(1-t)^2 t \mathbf{P}_1$ $+3(1-t) t^2 \mathbf{P}_2$ $+ t^3 \mathbf{P}_3$
$\displaystyle = \sum_{k=0}^{3} {}_3 \mathrm{C}_k \ (1-t)^{3-k} \ t^k \ \mathbf{P}_k$
となる。
実数 $t(0 \leqq 0 \leqq 1)$ を1つ決めて,内分比 $m:n=t:(1-t)$となるように作った点が $\mathrm{P}(t)$ であった。
$t$ を0から1に動かしたときの軌跡である方程式 $\mathrm{P}(t)$ が3次ベジェ曲線である。
⑥一般化する
以上により, 一般の $n$ 次ベジェ曲線の数式は次のとおりである:
$$\displaystyle \mathbf{P}(t) = \sum_{k=0}^{n} {}_n \mathrm{C}_k (1-t)^{n-k}t^k \mathbf{P}_k$$