三角比の定義の本質の理解を解説します。
三角比の定義の値を定めるとき、相似な（直角）三角形に無関係に三角比の数式の値が定まることを解説します。この記事は、三角比の単元の初めにある、三角比の定義の本質の解説です。
特に、本質が問われる試験、例えば共通テスト、での直前チェック事項としてください。生徒からの質問例と回答もあります！
記事の内容は（高校生向け）の三角比の定義の解説です。三角比の定義の本質が理解できます！
目次
数学Iの三角比の定義とは
三角比の定義って何？という方は、必ず下のリンクをご覧ください。公式を暗記することができますよ。
ダンスしていますよー！（私のオリジナル中のオリジナルのアイデアです。）
そして、公式を深く理解するためには、この記事を読んでください。
三角比の公式の覚え方ない？ダンスしよう【三角比の定義】 | ますレッスン教室
こんにちは。早速ですが、三角比の単元の一番最初の公式をすぐに覚えられるでしょうか？もしくは、すぐに教えられるでしょうか？サインエー イコール 斜辺分の高さ などと…
ますレッスン教室 
三角比の定義を確認しておきます。
直角三角形ABCの角度の三角比（3つ）とは、次の数式で定まる値のことである。
- $\displaystyle \sin A = \frac{c}{a}$
- $\displaystyle \cos A = \frac{c}{b}$
- $\displaystyle \tan A = \frac{b}{a}$
直角三角形を考えるときは、指定された角度（ $A$ ）を左側に置き、直角を右側に置きます。対応する辺の長さを $a, \ b, \ c$ として、それぞれの三角比の定義の数式に代入することで値が定まります。
定義の解説は以上ですが、何も疑問に感じないでしょうか？
これ以降は、話を簡単にするために、$\tan 60^{\circ}$ で説明します。をしていきます。（tan が最も存在感が薄いみたいですので。）サインとコサインについても話は同じです。
三角比の定義に対する疑問こそが本質
三角比の定義を復習しました。どこに疑問を持つのでしょうか？
- 指定された角度を左側、直角を右側にして、直角三角形を置く。
- 辺の長さを2つ選び、分母（底辺の長さ）と分子（高さの長さ）に置く。
- そして、角度 $A$ の前に、$\tan$ の記号を付ける。この値は、②で求めた辺の長さの比である。
以上が手順ですね。疑問は見つかりましたか？
この3つの手順に疑問を持って欲しい箇所はありません。手順以前の問題に疑問を抱いて欲しいです！
直角三角形は、いつからありましたか？
直角三角形は、誰が決めましたか？
例えば、$\tan 60^{\circ}$ を求める場合、$A=60^{\circ}$, $C=90^{\circ}$ （ $B=30^{\circ}$ ）の直角三角形を考えます。しかし、この条件を満たす直角三角形は沢山あります。相似な三角形の分だけ沢山あります。
抱いてほしい疑問とは、次の疑問です。
三角比の定義の本質の解説
相似な三角形で大きさの異なる三角形で三角比を計算してしまうと、$\tan 60^{\circ}$ の値が違う値になってしまうのではないか？
疑問に答える形で、三角比の定義の本質を解説します。
三角比の定義と相似な三角形
相似な三角形は中学校で勉強します。相似の定義を、そもそも確認しておきます。
三角形に限らず 2つの図形が相似な関係であるとは、一方の図形を拡大もしくは縮小することで合同な関係になることを言います。
合同な関係とは、一方の図形を回転、平行移動、裏返しをすることで、他方の図形とピッタリ重なる性質のことです。
相似とは「大きさが違うだけで形が一緒」ということですね。
ここから図形を三角形に限定します。中学校のときに、2つの三角形が相似であるための相似条件を習いました。覚えていますか？
- 3組の辺の長さの比が全て等しい。
- 2組の辺の長さの比と、その間の角の大きさがそれぞれ等しい。
- 2組の角の大きさがそれぞれ等しい。
『相似条件が条件が成り立つ $\Longrightarrow$ 2つの三角形は相似である』
ということです。しかし、この逆が（もちろん）成り立ちます。
『2つの三角形が相似である $\Longrightarrow$ 相似条件が成り立つ』
2つの三角形が相似であれば相似条件で言われていることが成り立ちます。今回は、三角比の定義の本質の疑問に回答するために①の相似条件に注目します。
整理すると『2つの相似な三角形の対応する辺の長さの比は全て等しい』が成り立つ。この共通の比（相似比という）を $k$ とすると、$a' = ka$, $b' = kb$ , $c' = kc$ が成り立ちます。
相似でも三角比の定義の値が一致する
2つの三角形 ABC と A'B'C' が相似であるとします。
相似比が $k$ だとしましょう。次が成り立ちます。
確かめたいことは、どちらの三角形で三角比を計算しても同じ値になるかどうかです！
三角形ABCと三角形A'B'C'のそれぞれで三角比を計算してみます。（タンジェントで計算してみます。）
三角形ABCで計算すると、そのまま $\displaystyle \tan A = \frac{b}{a}$ です。
次に、三角形A'B'C'で計算してみましょう。
いかがでしょうか？どちらの三角形で計算しても、$\tan A$ も $\tan A'$ も $\displaystyle \frac{b}{c} = \frac{b'}{c'}$ という同じ値になりました。
三角形が違っても、相似である限り、三角比の定義の値は違う数値にならないことが確認できました。他の三角比のサインとコサインでも同様です。三角比の定義の本質です。
相似な三角形と三角比の定義の具体例
イラストを2枚作成したので、$\tan 60^{\circ} = \sqrt{3}$ であることが、相似な直角三角形に依らず定まることを確かめましょう。
1枚目のイラストは、$\tan 60^{\circ}$ を求めるための直角三角形が正三角形を半分にして出来た形であることと、定義の計算をしています。
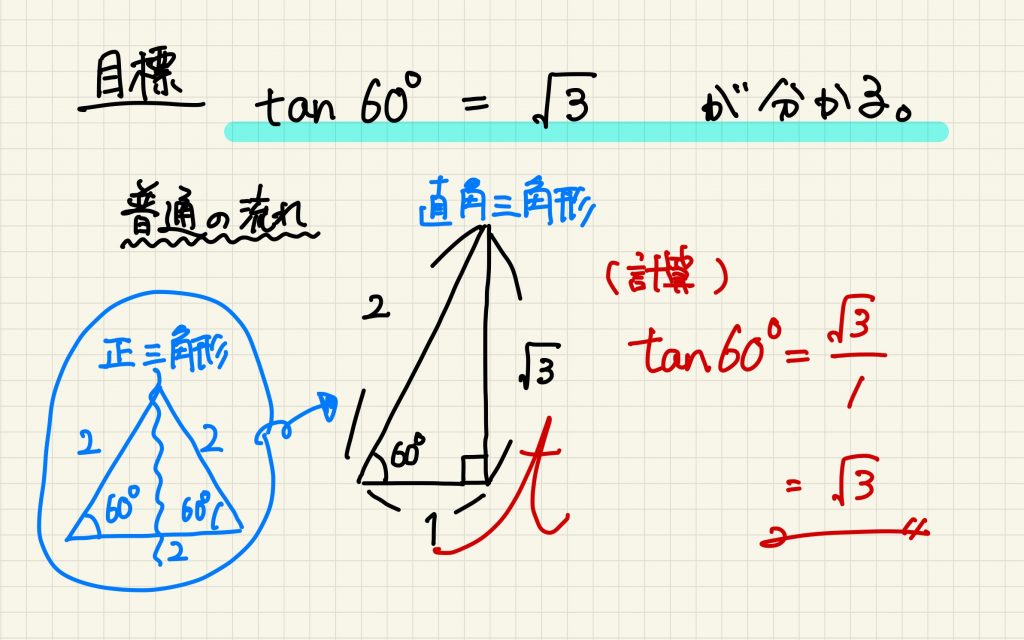
2枚目のイラストは、大きさの違う2つの相似な三角形（ $1:2$ の相似比 ）があったときに、$\tan 60^{\circ}$ の値が一致することを具体的な数値で確かめています。
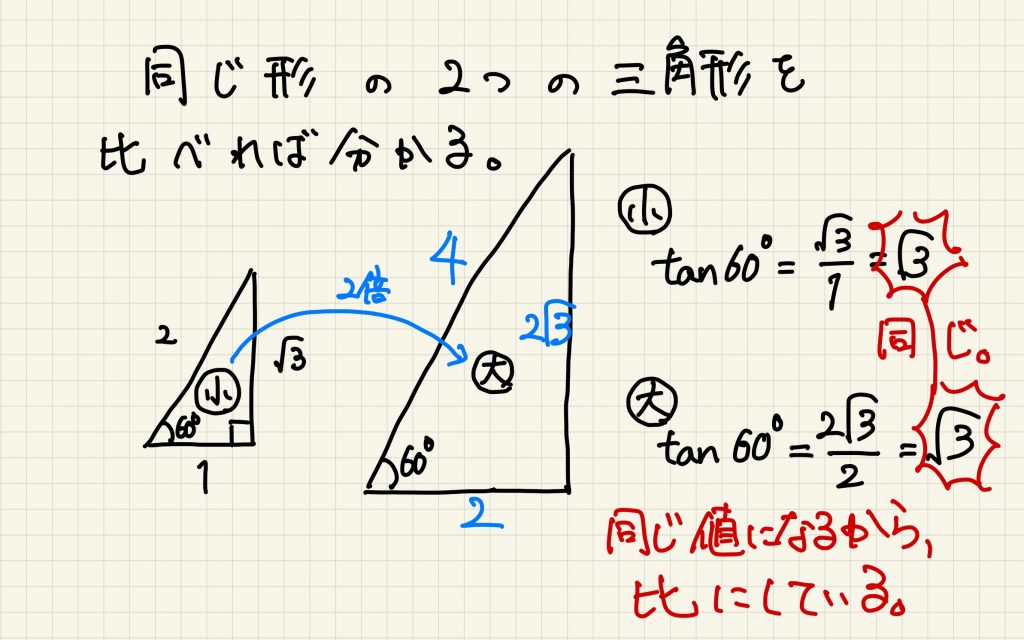
あなたも、サインやコサインも含めて、他の三角比においても、直角三角形の大きさに依らず、三角比の値が決まることを確かめてみてください。
三角比の定義の本質を理解しての質問と疑問
三角比は直角三角形の大きさに依らず値が定まることを確認してきました。この文章から何が分かるでしょうか？このように三角比の定義を決めた意義を感じていますか？
今までの内容が理解できていれば、生徒からよく挙がる疑問に答えることができます！
-
三角比の公式って、なんで分数の形（複雑な形）をしているの？
-
角の大きさと辺の長さを繋げるための数式としては、分数の形が最も合理的（かつシンプル）だからです。
つまり、$\sin A = a$ のような式だと、考える直角三角形に依って値がバラバラになってしまいます。しかし、辺の長さを比にすることで、相似比の違いは、約分という計算によって気にしなくてよいことになります。
三角比の定義は複雑な形をしているように見えて、角度と辺の長さを結びつける最も合理的な式なのです！角度と辺の長さが、分数という一工夫だけで結びつけられるています。見方を変えれば、非常にシンプルに表現できている式だと感じることができます。
-
相似な三角形に依らず決まることは分かったけど、それって何かの役に立つの？
-
めちゃくちゃ良い質問ですね。相似な三角形に関係なく三角比が決まることを解説しました。言い換えると、相似な三角形であれば、どの三角形で三角比を計算しても良い、ということです。
現実世界で現れる大きな直角三角形（木の高さを測るときとかに出くわす）の辺の長さや角度を調べるときに、もっと小さい、手のひらに収まる（相似な）三角形で計算を代用できる、ということになります。
めちゃくちゃ大きな対象であって計算が手に負えないように見えても、取り扱い可能な対象に代用できるということです。
以上の感じで、2つのQ&Aを終えます。1つ目の質問は、生徒からよく聞きます。2つ目の質問は、未だかつて生徒から出たことはありませんが、大切なことですので、Q&Aの形で記しました。
三角比の定義の本質解説のまとめ
本記事での解説内容をまとめます。
三角比の定義は、角の大きさと辺の長さ（の比）を結びつける画期的な数式である。定義の値を決めるためには、直角三角形を一つ用意する必要があるが、どの（相似な）直角三角形を用意しても問題なく、同じ値が定まる。辺の長さを比（分数）としていることは複雑に見えるけれども本質である。
以上で、角の大きさと辺の長さ（の比）を結びつける三角比の定義を理解することができました。三角比の定義の数式を導入することで、非常に大きな三角形であっても、小さいな三角形であっても、取り扱い可能な（相似な）三角形にすることで扱うことができる素晴らしさがあります。
ここまで、お読みいただき、ありがとうございます。
次のリンクは、三角比の単元の全体像を整理した記事です。
