- 表紙
- まとめ
- 具体例
- 理解
- Python
- 期末試験

目次
参考文献
アートで魅せる数学の世界
著:岡本健太郎
出版社:技術評論社
Wikipedia
まとめノート
「ドラゴン曲線🐉」とは
龍の見た目をしたフラクタル図形のこと。
定義
集合 $\mathbb{D}_{0} \subset \mathbb{C}$ と複素関数 $f_1$, $f_2$ について, 集合 $\mathbb{D}_{n} \subset \mathbb{C}$ を次のように帰納的に定義する. $$\mathbb{D}_{n} = f_1(\mathbb{D}_{n-1} ) \cup f_2( \mathbb{D}_{n-1} )$$ 極限集合 $\displaystyle \lim_{n \to \infty} \mathbb{D}_{n}$について, 龍の形に見えるものをドラゴン曲線という.
A. ヘイウェイ・ドラゴン
初期集合 $\mathbb{D}_0 = \{ 0 , \, 1 \}$ と, 次の複素関数を使う.
$\displaystyle f_1(z) = \frac{1 + i}{2}z$, $\displaystyle f_2(z) = 1 - \frac{1 - i}{2}z$
B. ツイン・ドラゴン
初期集合 $\displaystyle \mathbb{D}_0 = \{ 0 , \, 1 , \, 1-i \}$ と, 次の複素関数を使う.
$\displaystyle f_1(z) = \frac{1 + i}{2}z$, $\displaystyle f_2(z) = 1 - \frac{1 + i}{2}z$.
計算
定義
初期値の集合$\mathbb{D}_{0}$ と, 複素関数 $f_1$, $f_2$ によって, 曲線の形状が変わる。
A
ヘイウェイ・ドラゴンのイラスト
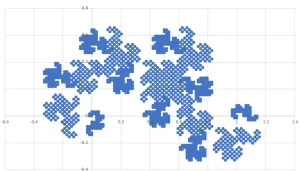
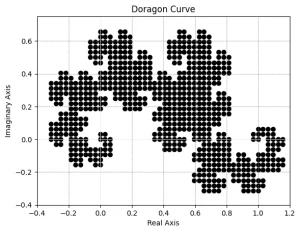
ドラゴン曲線の具体例
ヘイウェイ・ドラゴン

他のドラゴン曲線

アルゴリズム
ドラゴン曲線というフラクタル図形があります。
「アートで魅せる数学の世界(著:岡本健太郎)」という書籍で知って、Wikipediaの「ドラゴン曲線」のページで概要を知りました。
ドラゴン曲線の理解
今回は、ヘイウェイ・ドラゴンの描かれ方のアルゴリズムを解説します。
ドラゴン曲線の成長過程
第1世代
初めは2つの点と、1本の線分だけから始まります。
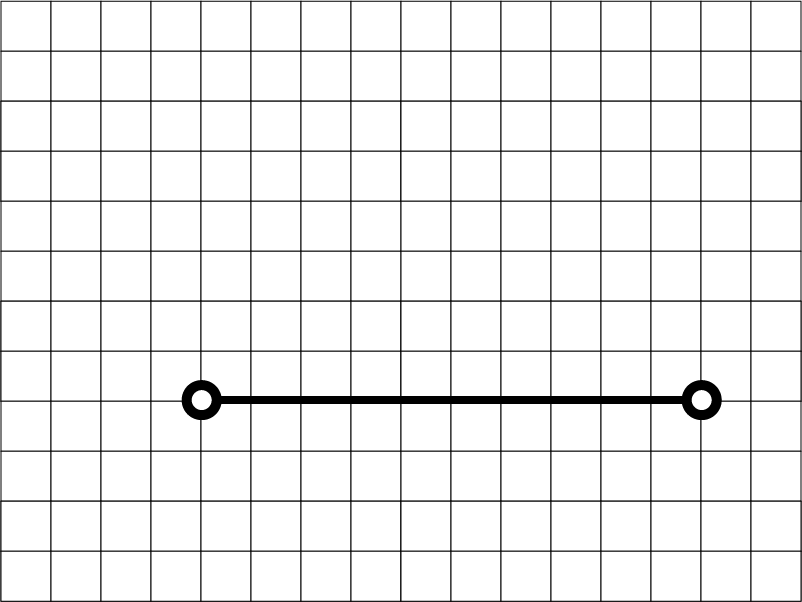
②第2世代
黄色の線分が(さっきの)第1世代の曲線です。
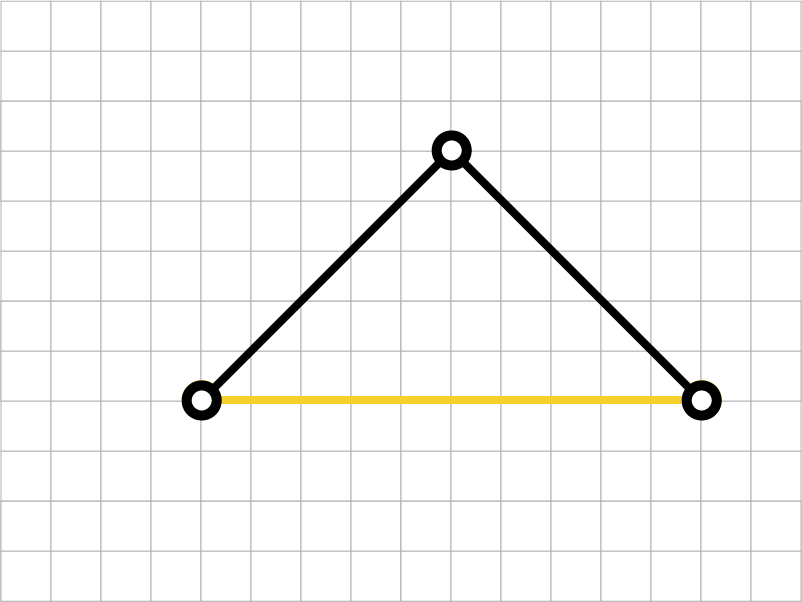
黒い線分が、第2世代の曲線です。
③第3世代
黄色の線分が(さっきの)第2世代の曲線です。
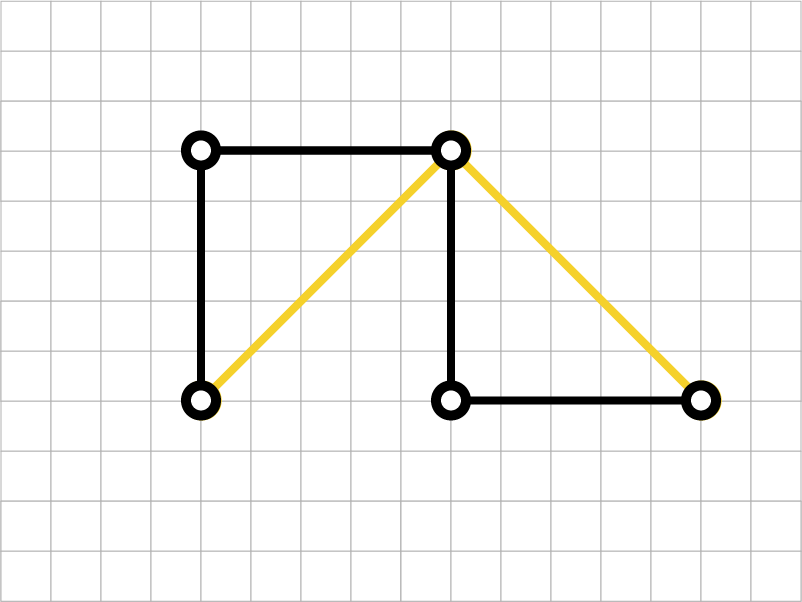
黒い線分が、新しい第3世代の曲線です。
第4世代
黒線部分が新しい第4世代のドラゴン曲線です。
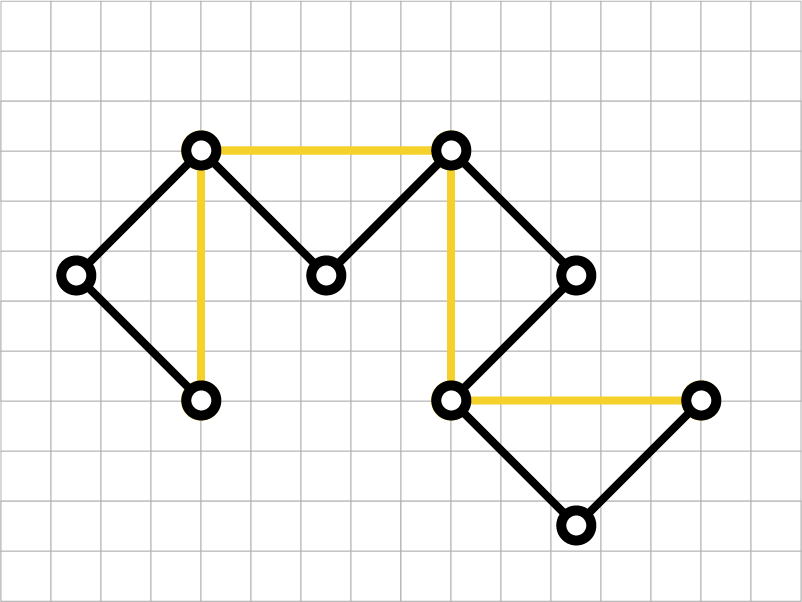
第5世代
黒線部分が新しい第5世代のドラゴン曲線です。
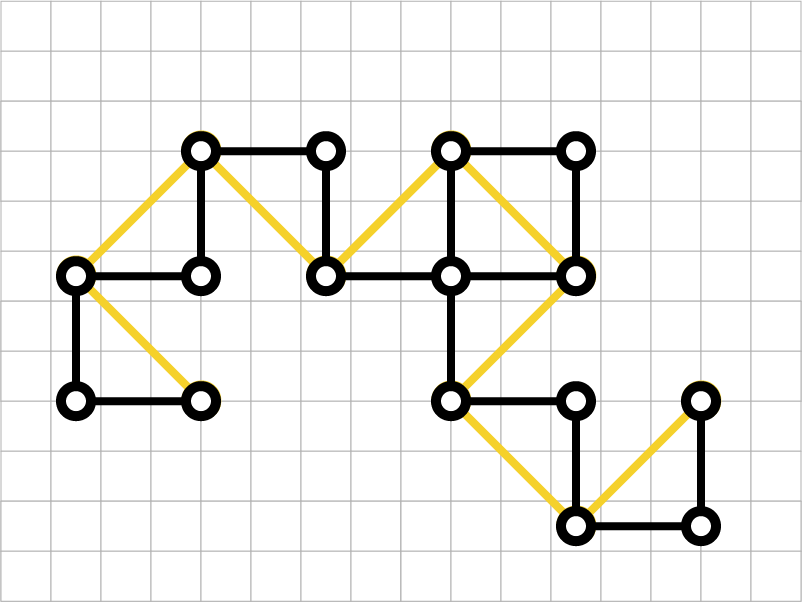
第6世代
黒線部分が新しい第6世代のドラゴン曲線です。
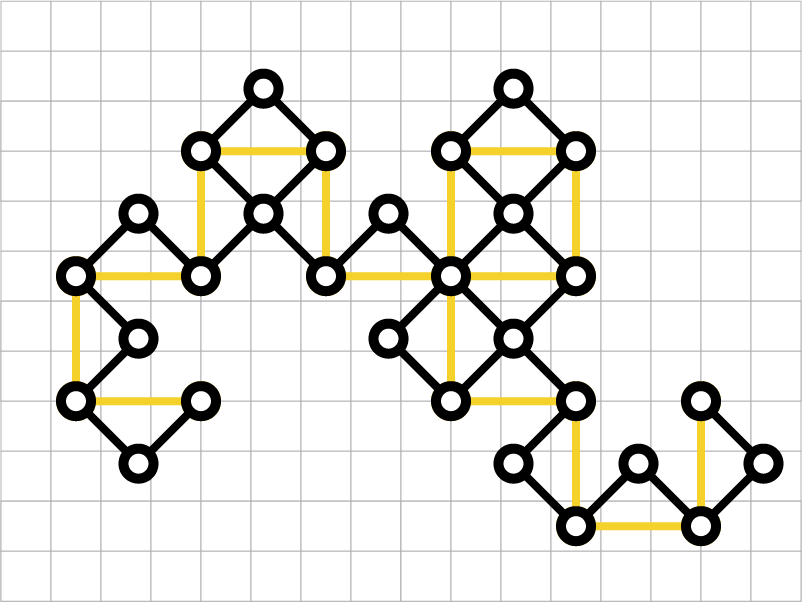
こういった作業を繰り返して、ドラゴン曲線を成長させます。
ヘイウェイ・ドラゴンの描き方
前の世代の線分を2本に分けていきます。このとき、できあがった2本の線分は90度で交わるようにします。
2本の線分を作る向きがポイントで、前の世代の曲線に対して、左→右→左→右→・・・の順番で線分を増やしていきます。
第1世代→第2世代
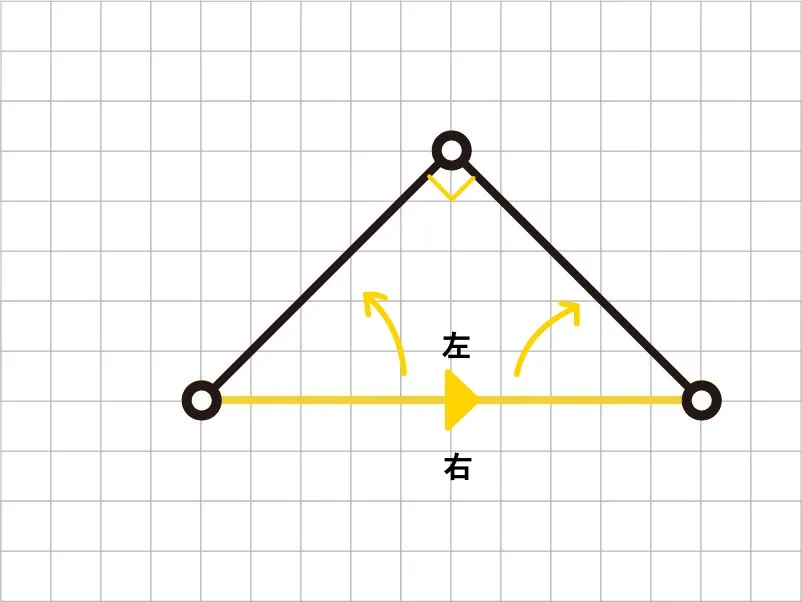
第1世代のもともとの線分の右側に直角二等辺三角形を作るイメージで、2本の線分に変形します。
このようにして第2世代になります。
第2世代→第3世代
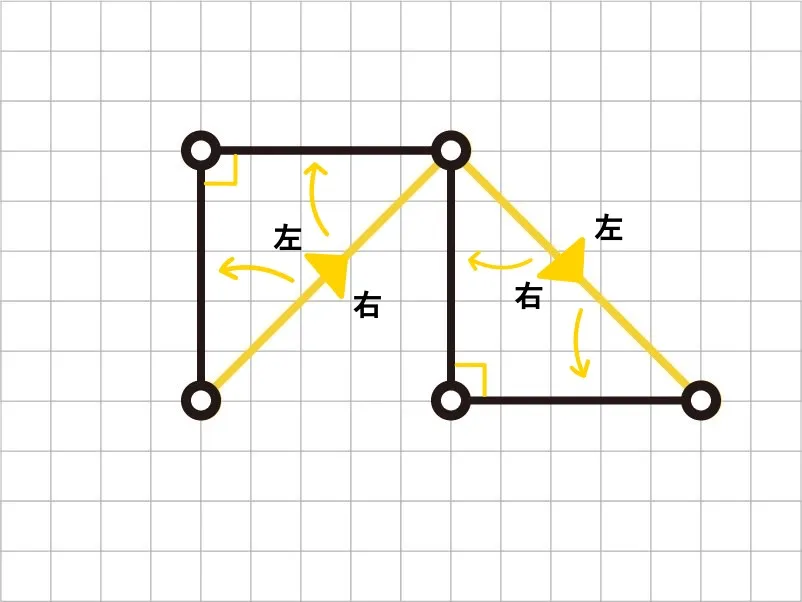
第2世代の1本目の線分には左側に直角二等辺三角形を作るイメージで、2本の線分に変形します。
2本目の線分には右側に直角二等辺三角形を作るイメージで、2本の線分に変形します。
このようにして第3世代になります。
第3世代→第4世代
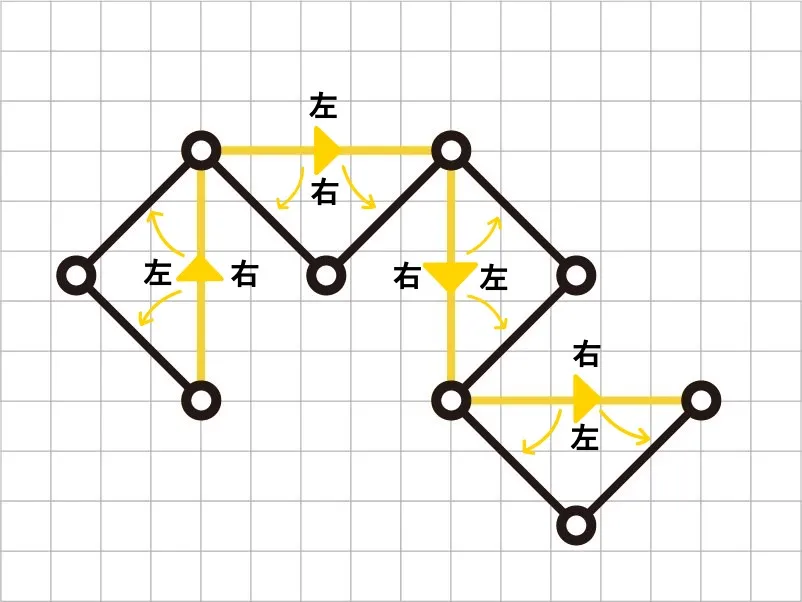
第3世代の1本目の線分には左側に、2本目には右側に、3本目には左側に直角二等辺三角形を作るイメージを持ちます。
それぞれ2本ずつの線分に変形します。
このようにして、第4世代になります。
この作業の繰り返しで、より世代を大きくして、龍の形ができていきます!
Python
ドラゴン曲線というフラクタル図形があります。
「アートで魅せる数学の世界(著:岡本健太郎)」という書籍で知って、Wikipediaの「ドラゴン曲線」のページで概要を知りました。
「アートで魅せる数学の世界」ではExcelでドラゴン曲線を作成していたので、今回はPythonで作成してみました。
ドラゴン曲線をPythonで作成
ドラゴン曲線のイラスト
ドラゴン曲線には、いくつかの種類があります。ここではヘイウェイ・ドラゴンを作成します。
ドラゴン曲線には「世代」という概念があります。定義のアルゴリズムの回数を1つ重ねることを世代でカウントしています。
第11世代のヘイウェイ・ドラゴンをPythonで作成したものです。
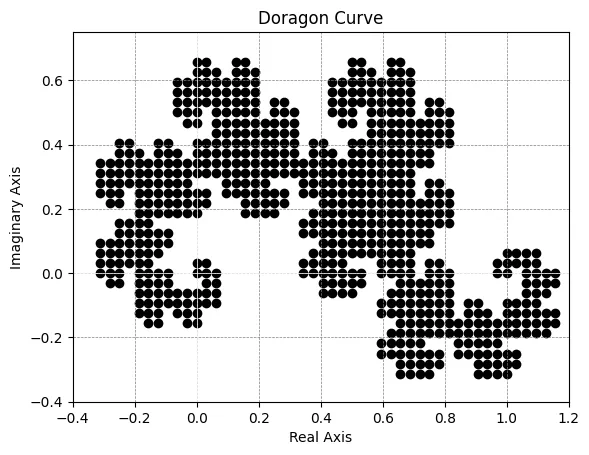
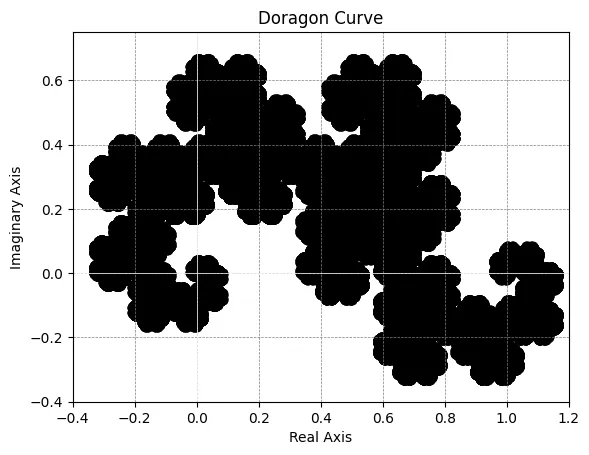
気まぐれで白黒反転させてみました。
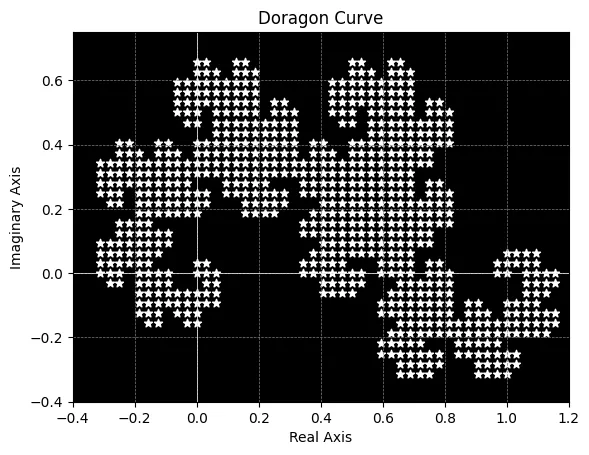
世代を上げて、第21世代のヘイウェイ・ドラゴンを作成しました。
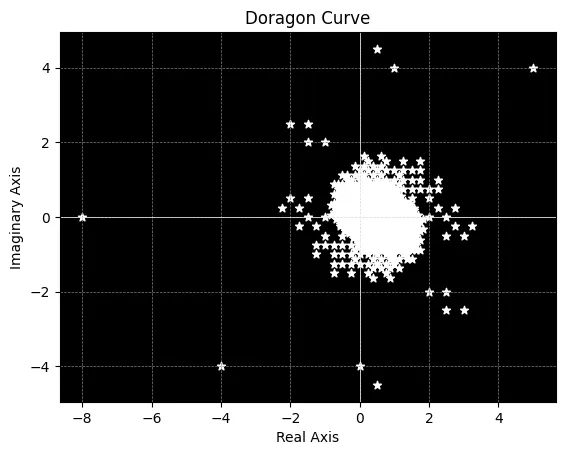
あと、ツインドラゴンという曲線を作成していたときに、偶然できた図を掲載します。
綺麗な銀河系みたいな図ができました🐲🐲。
ドラゴン曲線のPythonコード
紹介してきたドラゴン曲線のコードを掲載します。
「#世代」のgenerationの値を変えることで、より複雑なヘイウェイ・ドラゴンを作成することができます。
import matplotlib.pyplot as plt
import numpy as np
#関数の定義
def doragon1(z1):
f1 = (1+1j)/2*z1
return f1
def doragon2(z2):
f2 = 1- (1-1j)/2*z2
return f2
# 世代
generation = 11
# 初期集合
doragon = {0, 1}
for i in range(generation-1):
new_pts = set()
# 反復計算
for z in doragon:
z1 = doragon1(z)
z2 = doragon2(z)
new_pts.add(z1)
new_pts.add(z2)
doragon = doragon.union(new_pts)
print(doragon)
# 実部と虚部の取得
real_values = [np.real(z) for z in doragon]
imag_values = [np.imag(z) for z in doragon]
# 複素数平面への図示
fig, ax = plt.subplots()
ax.scatter(real_values, imag_values, color='white', marker='*')
ax.axhline(0, color='white', linewidth=0.5)
ax.axvline(0, color='white', linewidth=0.5)
# 背景色を白に設定
fig.patch.set_facecolor('white')
ax.set_facecolor('black')
plt.grid(color = 'gray', linestyle = '--', linewidth = 0.5)
plt.xlabel('Real Axis')
plt.ylabel('Imaginary Axis')
plt.title('Doragon Curve')
plt.xlim([-0.4, 1.2]) # 横軸の範囲を設定
plt.ylim([-0.4, 0.75]) # 縦軸の範囲を設定
plt.show()エクササイズ(高3期末試験《2023年2学期》)
理屈っぽい性格のAと感覚的な性格のBと,楽観的な後輩中学生のCが,塾で受験勉強している。
A:ねーね,この絵を見てよ。何に見える?私は桜に見えるかな。
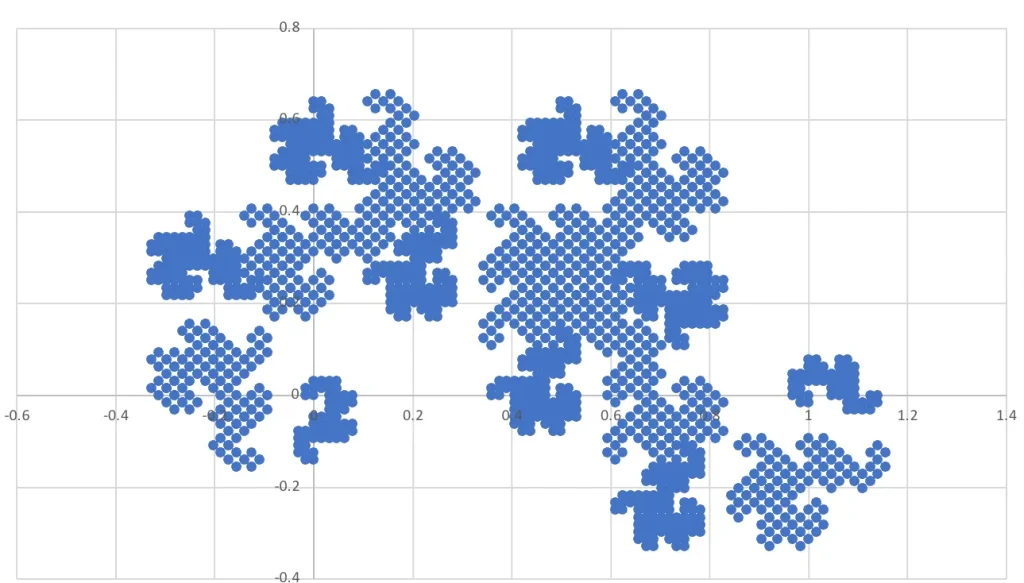
B:私は「竜です。」、竜に見えるよ♪
C:「ひき肉です。」
A:やっぱり勘がいいね。これは『ドラゴン曲線』って言うんだ。もっと詳しく言うと,この絵は『第13世代のドラゴン曲線』なんだ。
B:何それ?なんかカッコいいね!ドラゴンが成長してるってこと?
A:そうなんだ。この前,仕組みを勉強したから,教えるね。このドラゴン曲線は,はじめは2つの点からできてるんだ。複素数の $0$ と $1$ をスタートにして,$f_1$ と $f_2$ で全て変換した点達が次の世代のドラゴン曲線なんだよ。
$$f_1(z) = \frac{(1+i) \cdot z}{2}, \ \ f_2(z) = 1 - \frac{(1-i) \cdot z}{2}$$
B:この龍って、複素数の仕組みでできるんだー。不思議だ。フラクタルだな🎵
***
自然数 $n \geqq 2$ について,集合 $\mathbf{D}_n$ を,
$$\mathbf{D}_n = \{ f_1(d) \mid d \in \mathbf{D}_{n-1} \} \cup \{ f_2(d) \mid d \in \mathbf{D}_{n-1} \}$$
と定義する。は第 $n$ 世代のドラゴン曲線を表す(複素数の)点の集合である。
[問1]第1世代のドラゴン曲線の点の集合を $\mathbf{D}_1 = \{ 0, 1 \}$ とする。第2世代のドラゴン曲線の点の集合 $\mathbf{D}_2$ を求めよ。つまり,
$$\mathbf{D}_2 = \{ f_1(0), f_1(1) \} \cup \{ f_2(0), f_2(1) \}$$
を求めよ。
[問2]第3世代のドラゴン曲線の点の集合を$\mathbf{D}_3$ とする。第3世代の点(集合の要素)であって,かつ,第2世代の点(集合の要素)ではない複素数をすべて答えよ。
[問3]ドラゴン曲線の世代を成長させていく操作(関数)である $f_1$ と $f_2$ の図形的な意味として不適切なものを次から2つ選び,記号で答えなさい。【完答】
- $f_1$ は $\mathbf{D}_{n-1}$ の点を,原点中心に45°回転させ,大きさを 1/2 に縮め,$\mathbf{D}_n$ を作る
- $f_1$ は $\mathbf{D}_{n-1}$ の点を,原点中心に-315°回転させ,大きさを $1 / \sqrt{2}$ に縮め,$\mathbf{D}_n$ を作る
- $f_2$ は $\mathbf{D}_{n-1}$ の点を,原点中心に-45°回転させ,大きさを縮小させ,原点で対称移動させ,実軸方向に+1だけ平行移動して,$\mathbf{D}_n$ を作る
- $f_2$ は $\mathbf{D}_{n-1}$ の点を,原点中心に135°回転させ,大きさを縮小させ,実軸方向に+1だけ平行移動して,$\mathbf{D}_n$ を作る
- $f_2$ は $\mathbf{D}_{n-1}$ の点について,大きさを縮小させ,実軸方向に+1だけ平行移動をして,原点中心に-45°回転させて,$\mathbf{D}_n$ を作る
[問4]第4世代のドラゴン曲線の点の集合を $\mathbf{D}_4$ を複素数平面に表した図として,最も適切なものを①~④の中から1つ選べ。ただし,黒点が $\mathbf{D}_4$ の点を表す複素数である。
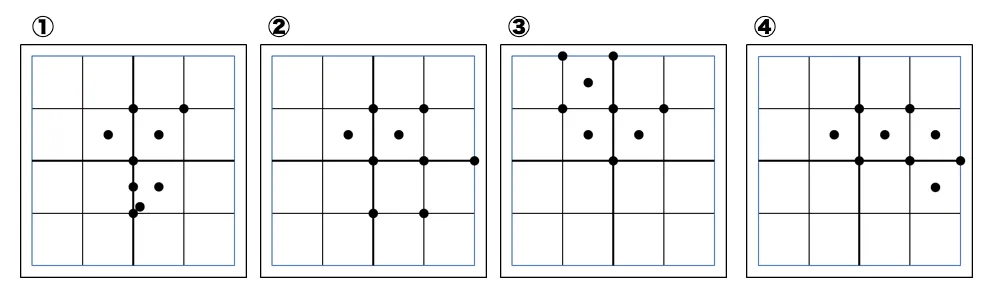
***
B:このドラゴンに、名前をつけない?
A:良いアイデアだね。んーー。ヘイウェイ・ドラゴンって名前はどうかな。
B:かっこいい、名前だね。このドラゴンと一緒に遊んでみたいね。
A:もう1つ点を増やそうよ?例えば,$1-i$ っていう複素数を増やしみよう。
***
[問5]複素数 $1-i$ について,変換 $f_1$(関数)を何度も繰り返す。つまり,$a_1 = 1-i$, $a_2 = f_2(a_1)$, $a_3 = f_1(a_2)$, $a_4 = f_1(a_3)$, ..., を考える。このとき,$a_1, a_2, a_3 \ldots$ は,実軸上に周期的に存在する。17回目に実軸上に存在するのは,第何世代のドラゴン曲線のときであるか答えよ。
***
B:うわっ。ヘイウェイ・ドラゴンが2匹いるよ。
A:いま調べたけど,このフラクタル図形を「ツイン・ドラゴン」って言うんだね。
B:ほかにも、数学のカオスの世界には、「レヴィ・ドラゴン」「ゴールデン・ドラゴン」「テルドラゴン」と呼ばれる曲線がいるみたいだよ。

C:レビィ・ドラゴンは、画像の中心を原点とした複素数平面として $-i$ をかけると、筋肉モリモリみたいなイラストになるね💪
B:フラクタルは生物の多様性とも関係しそう?!たくさん勉強してみたいな🎵
A:「他人に促されなくても努力する人間が一番成長する」ってことだね!
B:ドラゴン桜みたいな台詞だね。
A・B・C:たくさん勉強やってるから、かならず合格できるね!

