- 表紙
- 理解
- 意味
- コード
- まとめ
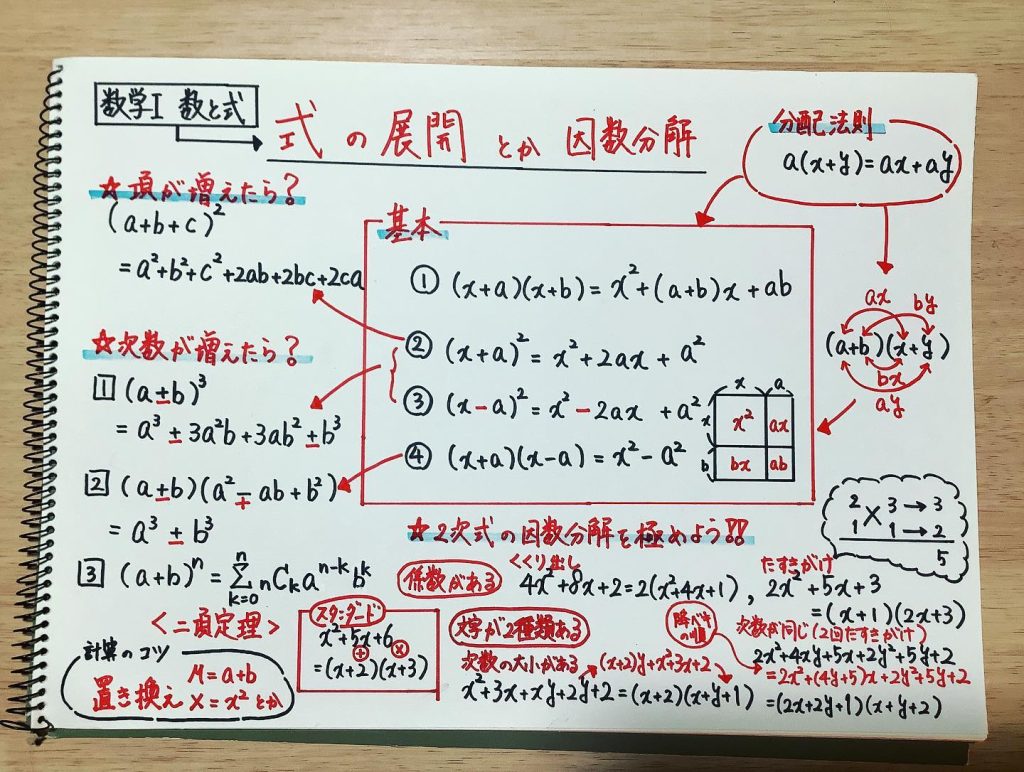
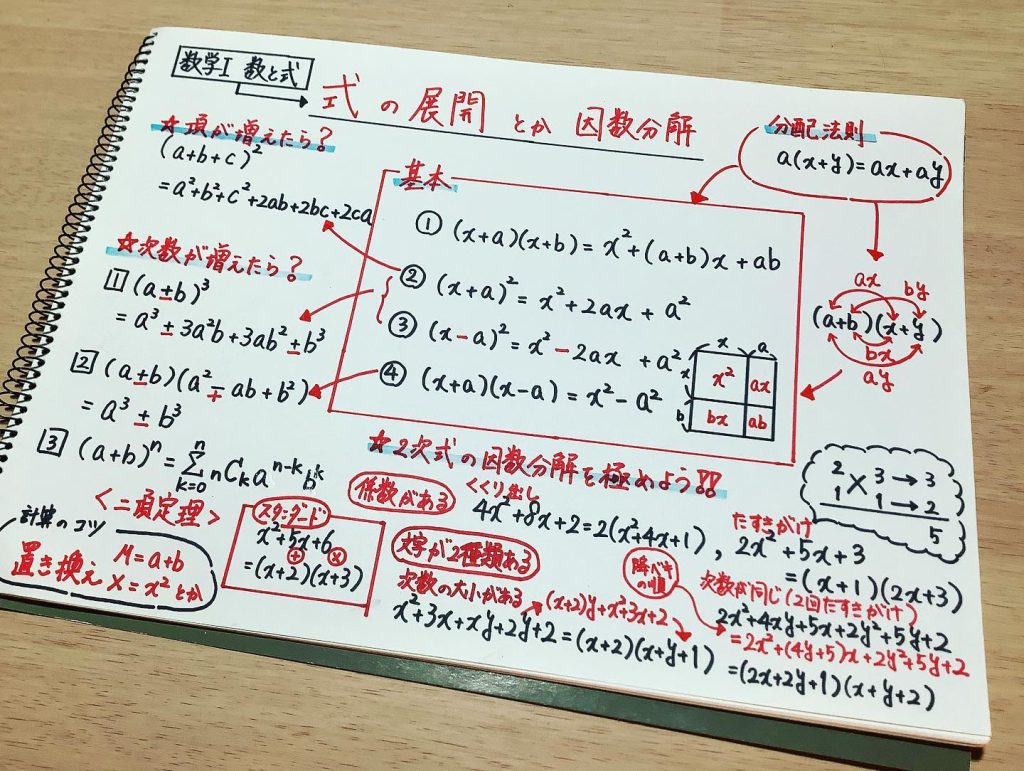
【理解】式の展開の数学
分配法則について
$a(x+y)=ax+ay$,
$(a+b)x = ax + bx$
Column. 分配法則の役割
2次式の展開について
$(x+a)(x+b)=x^2+(a+b)x+ab$
$(x+a)^2=x^2+2ax+a^2$
$(x-a)^2=x^2-2ax+a^2$
$(x+a)(x-a)=x^2-a^2$
$(a+b+c)^2$ $=a^2 + b^2 + c^2 + 2ab + 2bc + 2ca$
3次式の展開について
$(x+a)^3=x^3 + 3ax^2 + 3a^2x + a^3$
$(x-a)^3$ $=x^3 - 3ax^2 + 3a^2x - a^3$
$(x+a)(x^2-ax + a^2)$ $=x^3+a^3$
$(x-a)(x^2+ax + a^2)$ $=x^3-a^3$
$n$ 次式の展開について
$(x+y)^n$ $=x^n$ $+ {}_n \mathrm{C}_1 x^{n-1}y$ $+ {}_n \mathrm{C}_2 x^{n-2}y^2$ $+\cdots$ $+ {}_n \mathrm{C}_{n-1} xy^{n-1}$ $+ y^n$
$(x+y+z)^n$ の展開式の $x^py^qz^r$ の係数は $\displaystyle \frac{n!}{p!q!r!}$
$(x - y)(x^{n-1} +x^{n-2}y +\cdots +xy^{n-2}+y^{n-1})$ $=x^n-y^n$
$(x + y)(x^{n-1} -x^{n-2}y +\cdots -xy^{n-2}+y^{n-1})$ $=x^n+y^n$ ( $n$ が奇数のときのみ)
【意味】式の展開の意味
2次式の展開は長方形の面積としての意味をもつ

【遊び】折り紙で式の展開
折り紙で2次式の展開の図形的説明
折り紙で3次式の展開の図形的説明
【コード】Pythonで式の展開
四則演算(加減乗除)とべき乗 $a^b$ の計算方法
expand()による式の展開
まとめノート
「式の展開」とは
多項式の積を単項式の和で表すこと。
分配法則
$a(x+y) = ax + ay$
が成り立つ.
A. 乗法公式(2次式の展開)
- $(x+a)(x+b)$ $=x^2 + (a+b)x + ab$
- $(x+a)^2 = x^2 + 2ax + a^2$, $(x-a)^2 = x^2 - 2ax + a^2$
- $(x+a)(x-a) = x^2-a^2$
B. 乗法公式(3次式の展開)
- $(x + a)^3 =x^3 + 3ax^2 + 3a^2x + a^3$, $(x - a)^3 = x^3 - 3ax^2 + 3a^2x - a^3$
- $(x + a)(x^2 - ax + a^2)=x^3 + a^3$, $(x - a)(x^2 + ax + a^2) = x^3 - a^3$
C. 乗法公式($n$次式の展開)
- $(x+a)^n$ $\displaystyle = \sum_{k=0}^n {}_{n}\mathrm{C}_{k} x^{n-k} a^k$【二項定理】
- $(x - a)(x^{n-1} +ax^{n-2} +\cdots +a^{n-2}x+a^{n-1})$ $=x^n-a^n$
- $(x + a)(x^{n-1} -ax^{n-2} +\cdots -a^{n-2}x+a^{n-1})$ $=x^n+a^n$ ( $n$ が奇数のときのみ)
ポイント解説
基礎
分配法則を基本として, 交換法則と結合法則から各公式が導かれる。
A
面積の意味をもつ↓

+α
文字3つの展開公式↓
$(x+y+z)^2$ $=x^2+y^2+z^2 +2xy+2yz+2zx$
B
体積の意味をもつ↓


発展
ある条件のもと任意の関数 $f(x)$ を展開できる(テイラー展開):
$$f(x) = \sum_{n=0}^{\infty} \frac{f^{(n)}(0)}{n!}x^m$$