三角比の値を整理した!
平方根と分数で表すことができる有名角の三角比の値を計算して、整理しました。 目次三角比の表有名角の三角比鋭角の有名角($30^{\circ}$, $45^{\circ}$, $60^{\circ}$)$0^{\circ} […]
特殊相対性理論について
特殊等価原理と光速度不変を認めた、時空の物理学のこと。[1.特殊等価原理]:どの慣性系であっても, 同じ物理法則が成立.[2.光速度不変の原理]どの慣性系からも光速は一定.
信頼区間(推定)について
「信頼区間」とは 推定したい統計量が入っていると信頼できる区間のこと。 仮定 母集団が正規分布に従うとする. 母平均 $m$, 母標準偏差 $\sigma$ とする. 実際の標本の値を $x_1$, $\ldots$, […]
サイクロイドについて
直線上を転がる円上の1点がえがく軌跡のこと。[準備]半径 $a$ の円が直線上の原点Oの場所にある. 転がる円上の1点を動点P, 円の中心をCとする. 点Pは, 初めは点Oの位置にあるとする.
【Python】形態素解析(品詞分解)
形態素とは、ざっくりと言って「品詞」のことです。 英語で品詞は token , 品詞分解は tokenize です。 目次形態素解析のコード(Python)Pythonコード実行結果 形態素解析のコード(Python) […]
データの尺度水準について
利用可能な統計処理かを判断できるデータの性質の区分のこと。[質的データ]数値はラベルであり, 数値自体に意味はないデータのこと. [量的データ]数値で定義され, 数値自体に意味があるデータのこと.
メルカトル図法で地図をちょっと計算してみた
メルカトル図法の地図の作り方の数学をちょっと計算してみました。 目次地図と経度と緯度の関係地球上の地点 $S(u, v)$ の表現メルカトル射影地図作りの例を計算してみよう 地図と経度と緯度の関係 メルカトル図法で地図を […]
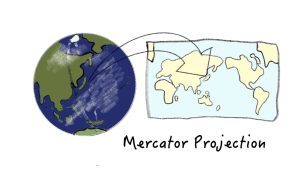
メルカトル図法って何か調べてみた
地図で作り方で有名なメルカトル図法のメリット・デメリットと、歴史を調べてみました。 目次メルカトル図法の常識メルカトル図法の採用メルカトル図法の歴史常識のまとめ メルカトル図法の常識 メルカトル図法の採用 メリット ※等 […]
メルカトル図法について
コンパスで同方向に進む経路が、直線で表現される地図のこと。[準備]$x \in ( -\pi/2, \ \pi/2)$ について, 次を逆グーデルマン関数と呼ぶ: $\mathrm{gd}^{-1}(x)=\mathrm{arsinh}\circ \tan(x)$
廿日市の佐方八幡神社の堀田仁助さんの灯篭を道標に
広島県の廿日市市(はつかいち市)は、厳島神社がある市です。 廿日市市は伊能忠敬に先駆けて測量をしていた天文学者の堀田仁助さんが生まれた場所です。 宮島から少し離れた場所に佐方八幡神社があります。 佐方八幡神社には、堀田仁 […]